Dokumendid > Keemia > Füüsikaline > Valitud peatükke elektrokeemiast

Kordamisküsimused

1. Laetud piirpindade üldised omadused

Adsorptsioon faasidevahelisel piirpinnal

Üheks kõige iseloomulikumaks protsessiks, mis on seotud uue faasidevahelise pinna moodustumisega, on adsorptsiooniprotsess. Tingitud on see sellest, et lähtuvalt osakeste erinevast energeetilisest seisundist lahuse sisemuses ning piirpinnal tekib kontsentratsioonigradient. Olgu aine i kontsentratsioon faasi sisemuses c_i ⁰ ja piirpinnal c_i.

Molekulid faasi sees mõjuvad teistele osakestele igas suunas võrdselt (kuna on faasi sees). Pindkihi molekulid - energeetiliselt kauslikuma oleku saavutamise soov > võimalikult väike pindala. Adsorbent, adsorbaat. Adsorptsiooniline side: 1) vdw side - madal sidemeenergia, u 5-10 kJ/mol e füüsikaline adosrptsioon (vesinikside pigem siin all); pöörduv, toimib kiirelt ka madalatel T-del; näide: metaani/vesiniku salvestamine metallihüdriididesse/süsinikmaterjali; 2) tugev keemiline side (nt iooniline, kovalentne, koordinatiivne) e kemosorptsioon; toimub kõrgematel T'del, sõltub adsorbendi keem loomusest, pöördumatu.

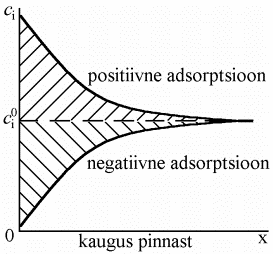Positiivne adsorptsioon tähendab, et antud osakestel on kasulik olla faasidevahelisel piirpinnal (näiteks hüdrofoobsed orgaanilised ühendid, see on süsivesinikradikaal tõrjutakse lahusest välja faasidevahelisele piirpinnale, polaarsed rühmad jäävad aga lahuse sisemusse).

Negatiivne adsorptsioon tähendab seda, et osaksete pindkontsentratsioon on väiksem kui faasi sisemuses, kuid tuleb rõhutada, et osakese pindkontsentratsioon on alati positiivne suurus. Negatiivne adsorptsioon esineb väga tugevasti hüdratiseeritud ioonide korral (Li⁺, ClO4^-).

Adsorptsiooniprotsess faasidevahelisele piirpinnale on kirjeldatav Gibbsi adsorptsiooni võrrandiga:

võrdeline komponentide mooliarvuga nii faasi sisemuses kui pindkihis (väljendatuna ühe pindalaühiku kohta)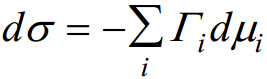

σ - uue pinna moodustumise pöörduv töö (s.t. töö, mida tehakse 1 m² uue pinna moodustamiseks tasakaalulistes tingimustes (J/m²; N/m). Tahke pind (tahke elektrood) - uue pinna moodustumise pöörduv töö; pind vedel (nt Hg) – pindpinevus. Γ_i – Gibbsi adsorptsioon (pindliig) (mooli/m²) μ_i – i-nda komponendi keemiline potentsiaal

Kui on tegemist kahe vedela faasi või vedela ning gaasifaasi kontaktiga, siis σ langeb kokku pindpinevusega. Kui aga üheks faasiks on tahke keha, siis pindpinevust ja uue pinna moodustumise pöörduvat tööd ei tohi samastada, kuna uue pinna moodustumise töö sõltub koordinaadist, suunast, millises toimub faasidevahelise piirpinna laienemine.

Seega kasutatakse vedelate elektroodide korral (Hg, Ga, Ga-sulamid) terminit pindpinevus, tahkete elektroodide korral aga tuleb eristada uue pinna moodustumise pöörduvat tööd σ ja pindpinevust γ.

Kui meil on tegemist kahekomponentse süsteemiga, millest kummalgi ei ole vaba elektrilist laengut (näiteks mingi orgaanilise ühendi vesilahus), siis on Gibbsi võrrand järgmise kujuga:

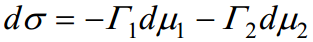
Kuna dμ₁ ja dμ₂ on täisdiferentsiaalid, siis

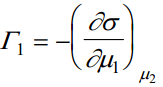
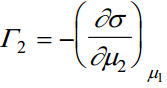
Nendest võrranditest tuleneb, et Γ₁ ja Γ₂ eksperimentaalselt mõõta ei saa, kuna μ₁ muutus kutsub esile μ₂ muutuse. Seega praktiliselt saab määrata σ muutust μ₁ muutumisel, kui samaaegselt muutub ka μ₂ . See on ekvivalentne täisdiferentsiaali dσ/dμ1 määramisega. Keemilised pot-id: u (neid eksperimentaalselt mõõta ei saa)

Vastavalt kahekomponentse süsteemi võrrandile:

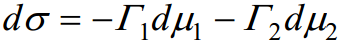
Saame

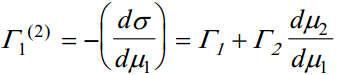suhteline pindliig teise komponendi suhtes

kus Γ₁ ⁽²⁾ on aine 1 suhteline pindliig aine 2 suhtes.

Arvestades Gibbs-Duhemi võrrandit, mis annab sõltuvuse keemiliste potentsiaalide ja lahuse koostise vahel:

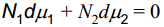i-nda komponendi moolide arv ja selle komponendi keem pot-i korrutis

võime eelmisel lehel toodud viimase valemi ümber kirjutada kuju

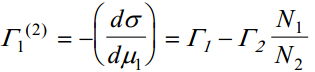aine 1 suhteline pindliig aine 2 suhtes

seob suhtelise pindliia tõeliste pindliigadega (eksp-lt mõõta ikka ei saa)

Saadud võrrand seob eksperimentaalselt määratava suhtelise pindliia tõeliste pindliigadega, kuid ei võimalda viimaseid määrata, kuna sisaldab kahte muutujat (ühe ja sama Γ₁ ⁽²⁾ väärtuse võib saada erinevate Γ₁ ja Γ₂ väärtustega).

Milline võiks siis olla Γ₁ ⁽²⁾ ja Γ₁ füüsikaline tagapõhi?

Oletame, et silindri abil, mis toetub oma põhjaga faasidevahelisele piirpinnale, on eraldatud mingi lahuse ruumala, kus esineb üleminekuala ühelt faasilt teisele.

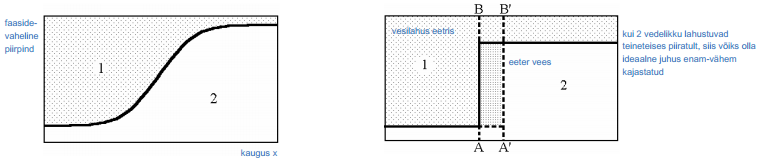
Joonisel 1 on kujutatud komponentide jaotus vastavalt kaugusele x faasidevahelisest piirpinnast reaalse süsteemi korral. Seda reaalset süsteemi kõrvutatakse ideaalse süsteemiga (b) mille korral komponentide jaotus ei sõltu kaugusest x. Selline juhus realiseerub juhul, kui kaks vedelikku lahustuvad teineteises piiratult, näiteks vasakpoolne osa kujutab endast vee lahust eetris ja parempoolne osa eetri lahust vees.

Olgu meil n₁ esimese komponendi kaaluline osa reaalses lahuses, n₁ ⁰ sama komponendi osa ideaalses lahuses. Kui silindri põhja pindala on S, siis vastavalt Gibbsi võrrandile on esimese komponendi pindliig avaldatav kujul

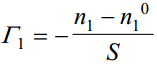
Tuleb rõhutada, et Γ₁ ei ole üheselt määratav, kuna tasapind on vabalt valitav. Kui muutub faasidevahelise piirpinna asukoht (näiteks tasandilt AB tasandile A’B’), siis muutub ka n₁ ning samuti Γ₁. Seetõttu tegi Gibbs ettepaneku fikseerida faasidevaheline piirpind kohal, kus ühe komponendi (näiteks komponendi 2) hulk reaalses süsteemis vastab selle komponendi hulgale ideaalses süsteemis, st n₂ ⁰ = n₂ . Sel juhul

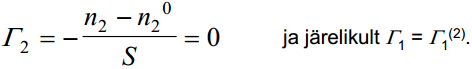
Sageli on praktilistest kaalutlustest lähtudes mõislik kasutada teistsugust Γ1(2) määratlust. Oletame, et faasidevaheline piirpind suurenes tasakaalulistes tingimustes 1cm2 võrra. Seejuures läheb faasi sisemusest piirpinnale (või negatiivse adsorptsiooni korral lahkub sealt) Γ1-ga võrdne kogus esimest ainet. Seega võib adsorptsiooni määratleda kui aine kogust, mida tuleb viia süsteemi juurde (või sealt ära võtta), et faasi koostis ei muutuks (μ1 = const; μ2 = const). Ka selliselt määratud Γ1 ei ole üheselt määratav, kuna μ1 ja μ2 võivad jääda muutumatuks ka juhul, kui viia juurde ka teist ainet. Seega aine 1 pindliig saadakse sel juhul, kui süsteemis muudetakse esimese aine hulka, teise aine hulk jääb aga samaks.

Näib, et metall–elektrolüüdilahus piirpinna jaoks võib Γ_i üheselt määratleda, kui samastada tinglik faasidevaheline piirpind elektroodi pinnaga. Tegelikkuses ei ole see lihtne, kuna seda piirpinda pole molekulaarses maastaabis võimalik vaadelda matemaatilise tasandina. Seetõttu on otstarbekas kasutada faasidevahelise piirpinna elektroodi pinnaga samastamise ligikaudset meetodit. Olgu kahekomponendiline süsteem (eetri lahus vees) kontaktis tahke elektroodiga ja kehtigu tingimus

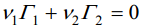
kus v₁ ja v₂ on 1. j 2. komponendi partsiaalsed moolruumalad.

Sel juhul fikseerivad võrrandid

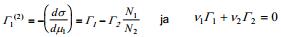
komponentide pindliiad Γ1(v) ja Γ2(v) vastavalt võrrandile

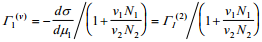
Kui nüüd eeldada, et lahuse ruumala adsorptsiooni tulemusena ei muutu, siis Γ₁ ^(v)-le vastab viirutatud ala pindala jooniselt 1.Viimasest vrrandist tuleneb, et aine 1 väikeste kontsentratsioonide korral ν₁ N₁ /ν₂ N₂ <<1,⇒Γ₁ ⁽²⁾≈Γ₁ ^(v) ning Γ₁ ⁽²⁾-le vastab samuti viirutatud ala pindala jooniselt 1, st et Gibbsi adsorptsiooni tasand, mille korral Γ₂ = 0, langeb ≈kokku elektroodi pinnaga.

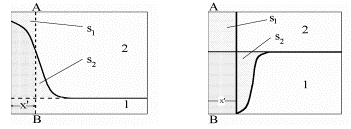
Kui tegemist on kontsentreeritumate lahustega, siis ν₁ N₁ /ν₂ N₂ <<1 ei realiseeru ning suhtelise adsorptsiooni mõiste muutub keerulisemaks. Sel juhul tuleb valida Gibbsi adsorptsiooni tasandi asukohaks kaugus x’, kus s₁ = s₂ ja seega Γ₂ = 0. Sel juhul x’ ei lange enam kokku elektroodi pinna asukohaga. Positiivse adsorptsiooni korral asub x’ lahuse sisemuses, negatiivse adsorptsiooni korral aga peab x’ asuma metalli sisemuses!

Vastavalt viimasele võrrandile on Γ_i ⁽²⁾ absoluutväärtuselt alati väiksem kui Γ_i ^(v). Seega ei lange pindliia või adsorptsiooni mõiste kokku pindkontsentratsiooni mõistega. Pindkontsentratsioon on alati positiivne suurus. Ta võib küll olla väiksem kui kontsentratsioon faasi sisemuses. Gibbsi adsorptsioon ehk pindliig aga võib olla ka negatiivne suurus. Üldiselt pakuvad elektrokeemia seisukohalthuvi süsteemid, mille korral pindliig lokaliseerub õhukese nn pindkihi piires ja kus realiseerub tingimus ν₁ N₁ /ν₂ N₂ <<1. Selliste süsteemide korral Γ_i ⁽²⁾≈Γ_i ^(v), see on pindliig langeb kokku pindkontsentratsiooniga. Selline juhtrealiseerub enamiku orgaaniliste ainete elektroodidel adsorptsiooni korral. Kuid üldjuhul on pindliia sidumiseks pindkontsentratsiooniga vaja sisse tuua mudelkujutlused adsorptsioonikihtide ehitusest.

2. Potentsiaalihüpped faasidevahelisel piirpinnal

1. Lihtsuse mõttes vaatleme esmalt piirpinda LAHUS–ÕHK

Kuna jõud, mis toimivad piirpinnale, see on pindmisele lahuse kihile õhufaasi ja lahusefaasi poolt, on tunduvalt erinevad, siis seetõttu erineb lahusti molekulide jaotus ja orientatsioon lahuse piirpinnal oluliselt lahusti molekulide kaootilisest jaotusest lahuse sisemuses. Selle tulemusena kujuneb lahuse pinnal välja molekulide eelistatud orientatsioon. Kui need molekulid on polaarsed, s.t. omavad dipoolmomenti, elektrilist laengujaotust, siis võib eelistatud orientatsiooni tekkimine viia ruumilise laengujaotuse väljakujunemisele piirpinnal.

2. Lahuses esinevad katioonid ja anioonid võivad olla erineva pindaktiivsusega ja selle tulemusena asuvad erineval kaugusel faasidevahelisest piirpinnast.

Tähistame potentsiaalide erinevuse piirpinnal lahus–õhk, mis on tingitud nii lahusti molekulide eelistatud orientatsioonist kui ka ioonide erinevast paiknemisest faasidevahelises piirkihis, suurusega χ^L. χ^L – lahuse pindpotentsiaal; on arvuliselt võrdne tööga, mis on vajalik ühikulise positiivse proovilaengu toomisel õhufaasist lahusefaasi sisemusse. Pindpotentsiaal, see on potentsiaalide erinevus, tekib samuti ka metall–lahus piirpinnal.

Metalli vabadel elektronidel on märgatav kineetiline energia, mille arvel väljub osa elektrone (s.o. elektrongaas) metalli ioonse skeleti, s.o. metalli ioonvõre raamidest. Kujuneb välja laengujaotus metalli üldjuhul positiivselt laetud ioonse skeleti ja sellest väljunud elektrongaasi vahel, mis tingibki potentsiaalihüppe χ^M piirpinnal metall|vaakum. Kokkuleppeliselt loetakse χ^M tinglikult suuremaks nullist.

Vaatleme alljärgnevalt uuritava faasi (metalli või lahuse) elektrilise potentsiaali seda osa, mis on tingitud antud faasi vabadest elektrilistest laengutest. Elektrostaatika alusel teame, et ühikulise proovilaengu viimiseks lõpmatusest ühtlaselt laetud metallist kera (raadiusega R ja laenguga q) lähedusse on vaja teha tööd

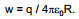
Selle töö suuruse määrab ära nn. metallifaasi välispotentsiaali suurus, mida tähistatakse ψ^M. Kuna ka lahuse pinnal võib olla teatud hulk vabu elektrilisi laenguid, siis ka ühikulise proovilaengu toomiseks lõpmatusest lahuse pinna lähedusse on vaja teha tööd, mille suurus on määratud lahuse välispotentsiaaliga ψ^L. Üldjuhul ψ^L 0.

Kerkib küsimus, millisel kaugusel metalli või lahuse pinnast on otstarbekas valida antud punkt. Metallist kera korral on potentsiaal kaugusel x määratud valemiga

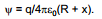
Seega punkt, mille kohal vaadeldakse ψ^M ja ψ^L, on vaja valida sellisele kaugusele, kus potentsiaal oluliselt ei erineks potentsiaalist faasi pinnal, s.o. kera korral

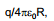
s.t., et kaugus x oleks palju väiksem kui kera raadius R, ehk teisti lähedal kera pinnale.

Teisalt on teada, et see suurus x peab olema küllalt suur, et täiendavalt ei peaks arvestama indutseeritud elektrostaatilisi lisajõude, mis võivad esineda laetud kera ja tema pinna läheduses asuva ühikulise proovilaengu vahel. Kõige kaugemale ulatuvateks nendest täiendavatest jõududest on nn. peegeldusjõud, mis on tingitud ühikulise proovilaengu ja tema poolt kera pinnal indutseeritud vastaslaengu vahelisest toimest. Seepärast valitakse punkt sellisele kaugusele x, et peegeldusjõud proovilaengu e₀ jaoks e₀/16πε₀x oleks väga väike võrreldes suurusega q/4πε₀R.

Metalli pindpotentsiaali ja välispotentsiaali summa on võrdne nn. metalli sisepotentsiaaliga:

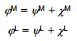
Need võrrandid kujutavad endast sisepotentsiaali – tööd, mida tuleb teha, et tuua ühikuline proovilaeng lõpmatusest (vaakumis) ühtlaselt laetud kera sisemusse, st. üldjuhul oleks potentsiaali erinevus kahe punkti vahel määratud tööga, mis on vajalik, et viia ühikuline elementaarlaeng ühest punktist teise. Kui mõlemad punktid asuvad samas faasis, siis on töö elektriline ning potentsiaalide vahe on vahetult mõõdetav või arvutatav. Kui need punktid aga ei asu samas faasis, siis töö ei ole ainult elektriline, sest nendes punktides ei tarvitse laetud osakeste keemilised potentsiaalid olla võrdsed.

Laetud osakese energeetilise seisundi väljendamiseks mingis faasi punktis on võetud kasutusele elektrokeemilise potentsiaali mõiste

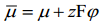
kus ϕ on osakese potentsiaal antud faasi punktis D – kaugel vaakumis asuva punkti suhtes. Nagu keemiline potentsiaal, on ka i-nda osakese elektrokeemiline potentsiaal määratud Gibbsi vabaenergia osatuletisega antud komponendi hulga järgi, s.o.

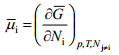
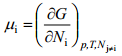
Kus

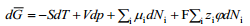
On hädatarvilik rõhutada, et vaadeldes nähtusi faasidevahelistel piirpindadel, tuleb ära märkida, millise faasi jaoks on meil määratud , ja ϕ. Selleks on võetud kokkuleppeliselt kasutusele ülemised indeksid, näiteks faasi α elektrokeemiline potentsiaal

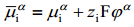
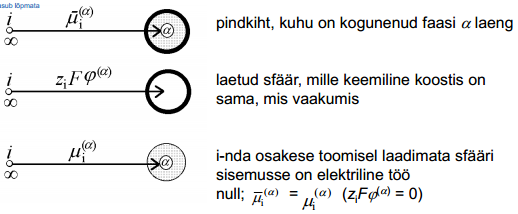Joonis: vasakul pool asub vaakum; i-ndas osake asub lõpmata kaugel.

i-nda osakese toomisel ∞ kaugel vaakumis asuvast punktist sellise seest tühja laetud sfääri sisemusse tehakse elektrilist tööd .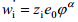

Korrutades selle töö Avogadro arvuga saame i-nda osakese elektrokeemilise potentsiaali elektrilise osa, s.o. z_iFϕ^α. Suurust ϕ^α nimetatakse faasi α sisepotentsiaaliks. Antud ϕ^α määratlus on õige ainult juhul, kui osake i ei reageeri faasiga α, s.o. vastastikune keemiline toime puudub.

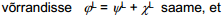
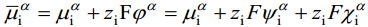
Eksperimentaalselt saame määrata aga ainult reaalse osakese ülekandmiseks tehtavat tööd, s.o. elektrokeemilist potentsiaali või siis elektrokeemiliste potentsiaalide erinevust kahe faasi vahel - . Eksperimentaalselt seda tööd elektrokeemiliseks ja keemiliseks lahutada ei saa. Mudeli abil saab aga situatsiooni analüüsida. Borni mudeli abil saab välja arvutada i-nda osakese keemilise potentsiaali lahuses, s.o. µ_i on leitav teoreetiliselt.

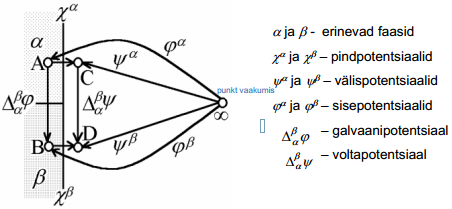
Kui kontakteeruvad 2 erineva koostisega faasi α ja β, mis võivad olla kaks erinevat metalli või metall ja elektrolüüt, siis punktide vahel, mis asuvad kumbki eri faasis, esineb potentsiaalihüpe, mida tähistatakse 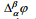ja nimetatakse galvaanipotentsiaaliks. Galvaanipotentsiaal kujutab endast tööd, mida tuleb teha ühikulise proovilaengu viimiseks faasist α faasi β, kusjuures proovilaeng ei tohi reageerida kummagi faasiga.

Voltapotentsiaali 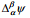, mis iseloomustab potentsiaalierinevust kahe faasi α ja β pindade vahetus läheduses, so punktide C ja D vahel (C ja D asuvad samas faasis, antud juhul vaakumis). Kuna ühikulise laengu üleviimise töö ei sõltu läbitud teest, siis võime kirjutada

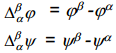
Eksperimentaalselt saab määrata ainult faaside α ja β elektrokeemiliste potentsiaalide erinevust.

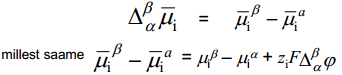
Siit tuleneb, et 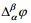on eksperimentaalselt määratav ainult siis, kui = , mida pole võimalik realiseerida. Samuti pole võimalik eksperimentaalselt määrata pindpotentsiaale. Eksperimentaalselt määratav on voltapotentsiaal, kuna punktid C ja D asuvad samas faasis.

Pindpotentsiaali tuleb eristada osakese väljumistööst , s.o. tööst, mida tehakse reaalse osakese i väljaviimisel faasist α punkti, mis asub α pinna lähedal vaakumis.

Väljumistöö erineb pindpotentsiaalist keemilise potentsiaali võrra.

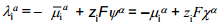
Erinevalt elektrokeemilisest potentsiaalist ja sisepotentsiaalist sõltuvad pindpotentsiaal ? ja osakese väljumistöö ?i faasi kristallograafilisest struktuurist.

Kahe erineva kristallograafilise orientatsiooni vahel esineb märgatav voltapotentsiaali erinevus (~100…500 mV).

Kuigi galvaanipotentsiaal pole eksperimentaalselt määratav, saame teha mõningaid järeldusi, kasutades elektrokeemilise tasakaalu püstitumise tingimusi.

Kui toimub laetud osakeste suunatud ülekanne ühest faasist teise, siis

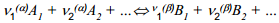
(A_i on faasi α osakesed, B_i on faasi β osakesed).

Elektrokeemilise tasakaalu korral

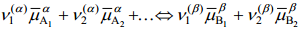
Kui faasidel α ja β on ainult üks ühine laetud osake (näiteks kaks erinevat metalli või metall sama iooni sisaldavas lahuses), siis elektrokeemilise tasakaalu korral:

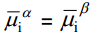
s.t. laetud osakese i liikumine toimub nii kontsentratsioonigradiendi kui ka elektrokeemilise potentsiaali erinevuse tõttu.

Vaatleme nüüd olukorda, kus alguses ei ole tasakaalu metalli ning tema ioone sisaldava lahuse vahel, s.o.

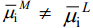
Pärast metalli sukeldamist lahusesse ja mõne aja möödumist 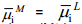. See protsess toimub nii metalliioonide liikumisel läbi metall–lahus piirpinna (M⁺ kas sadeneb metallile või metall lahustub) kui ka elektriliste laengute (elektronide) suunatud liikumise tulemusena (metall–vaakum piirpinnal toimub elektrongaasi väljumine metallist ja vabade elektrostaatiliste laengute kogunemine pindkihti).

Metall–lahus piirpinnal toimub seega galvaanipotensiaali muutus, mis on seotud nn. ioonse kaksikkihi moodustumisega. Selliselt moodustunud kaksikkihis esineb potentsiaalihüpe, mida tähistatakse Δϕ.

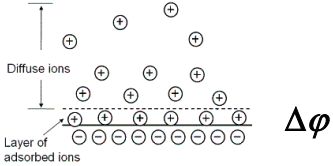Samuti määravad galvaanipotentsiaali metalli ja lahuse pindpotentsiaalid.

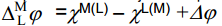
χ^M(L) ja χ^L(M) erinevad metalli ja lahuse pindpotentsiaalidest õhu suhtes, kuna metall–lahus kontakti korral ei välju elektrongaas mitte õhku vaid lahusesse, samuti on muutunud lahuse dipoolide orientatsioon metalli pinna läheduses, võrreldes lahus–õhk piirpinnaga.

Metalliioonide läbiminek metall–lahus piirpinnast ning vabade laengute üleminek ühe faasi pinnalt teisele määravad ära tasakaaluoleku ja selle saabumise tingimused, s.o. suurused χ^M(L)– χ^M ja χ^L(M)– χ^L. Pindpotentsiaalid on väga tundlikud laengute suhtes, samuti ka pindaktiivsete ühendite suhtes.

Iga metalli jaoks on põhimõtteliselt võimalik valida sellise koostisega lahus, kus ei toimu osakeste M⁺ suunatud liikumist. Selliseid lahuseid nimetatakse null-lahusteks, kus Δϕ= 0 ja galvaanipotentsiaali metall–lahus piirpinnal võib esitada kujul

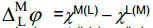
Vabade laengute puudumine metall–lahus piirpinnal ei tähenda veel, et vabad laengud puuduvad metall–õhk ja lahus–õhk piirpinnal. Seepärast ei saa teha järeldust, et nulllahustes on voltapotentsiaal metall–lahus piirpinnal null.

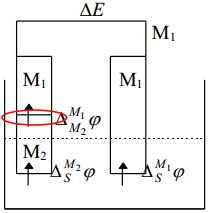Kui viia kontakti kaks erinevat metalli ühes ja samas elektrolüüdi lahuses, siis on eksperimentaalselt mõõdetav potentsiaalide erinevus avaldatav järgmiselt:

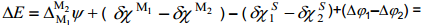
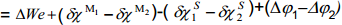
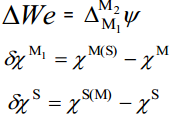
Kui aga võrdleme null-laengupunktide erinevusi erinevate metallide korral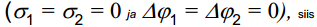

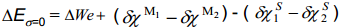
Et võrrelda metall-lahus-piirpinda metall-vaakum-piirpinnaga, peame teadma nn absoluutset vesinikelektroodi potentsiaali vaakumi suhtes, ehk

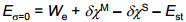On leitud, et E_st = 4.31 V. See tähendab, et Pt|H_ads|H₂O süsteemi potentsiaal vaakumi suhtes on väga suur; see potentsiaalide erinevus on esimeses lähenduses samastatav lahuse tõelise sisepotentsiaaliga vaakumi suhtes.

3. Põhilisi mudelettekujutusi elektrilise kaksikkihi struktuurist - Helmholtzi teooria

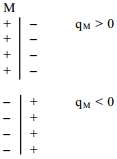Valitakse kaks vasksilindrit, mis on asetatud teineteise sisse. Sellise süsteemi väljatugevus ei sõltu koordinaatidest, kus asub osakene, kui silindrite kumerusraadiused on palju suuremad silindritevahelisest kaugusest. Antud süsteemi jaoks saadakse tasaparalleelse kondensaatori valem

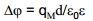
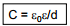
ε₀ – vaakumi dielektriline läbitavus

Definitsiooni järgi on vaakumi suhteline dielektriline läbitavus 1. Õhu korral on see 1,00054...1,0006 ja vee korral 34...88 (sõltub vee temperatuurist).

Suhtelise dielektriline läbitavuse kaudu saab leida keskkonna absoluutse murdumisnäitaja.

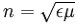
kus μ on keskkonna magnetiline läbitavus. Et enamiku ainete puhul μ on väga lähedal 1-le.

ε– antud keskkonna dielektriline läbitavus, d – kondensaatori plaatide vaheline kaugus, q_M – laengutihedus, Δϕ– potentsiaalide erinevus.

Helmholtzi teooriast järeldub, et potentsiaali jaotus elektrilises kaksikkihis on lineaarne, aga elektrilisest kaksikkihist väljaspool on potentsiaal konstantne.

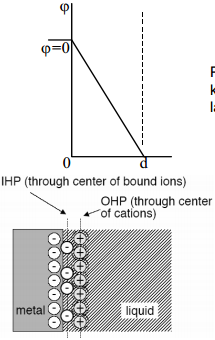Potentsiaalijaotus on elektrilises kaksikkihis kujutatav analoogiliselt joonisega ja avaldis laengutiheduse jaoks näeb välja järgmine:

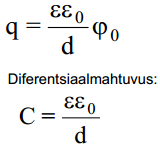
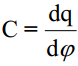
Võrrandist nähtub, et elektrilise kaksikkihi laeng sõltub lineaarselt elektroodi potentsiaalist ϕ₀. Üldjuhul esimeses lähenduses see järeldus ühtib eksperimentaalsete andmetega negatiivsete pinnalaengute alas.

Kasutades Lippmanni võrrandit:

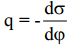
ja võrrandit

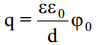
On võimalik saada seos pindpinevuse või uue pinna moodustumise pöörduva töö ja elektroodipotentsiaali vahel:

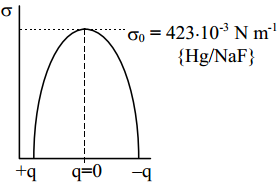
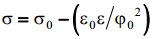kus σ₀ on integreerimiskonstant, mis on määratud null-laengupunktis E_q=0, see on σ₀ = σ, kui q = 0.

Vastavalt eelnevale võrrandile peab elektrokapillaarkõver omama tagurpidi pööratud parabooli kuju, mis, nagu eelpoolt teada, ühtib eksperimentaalsete tulemustega.

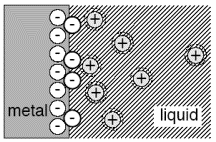
4. Põhilisi mudelettekujutusi elektrilise kaksikkihi struktuurist - Gouy-Chapmani teooria

Gouy teooria vaatleb lahuses esinevaid ioone kui matemaatilisi punkte, mis on pidevas soojusliikumises, osasid nendest tõmmatakse pidevalt elektroodi poole, samas ka tõugatakse eemale. Erandina Helmholtzi teooriast, osalevad ka elektroodi pinna läheduses asetsevad elektrilist kaksikkihti moodustavad ioonid soojusliikumises. Kuid anioonide ja katioonide jaotus elektrilises kaksikkihis ei ole ühtlane ning elektroodi laengu poolt tekitatud elektriväli, sõltuvalt pinnalaengust, soodustab kas anioonide või katioonide eelistatud kogunemist pindkihti, kui |q| ≠0.

Gouy teooria tuletamisel on tehtud kolm lihtsustust (eeldust):

Elektriväli elektrilises kaksikkihis on kirjeldatav Poissoni võrrandiga, kus ∇² on Laplace’i operaator ja ρon ruumiline laengutihedus.

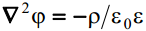
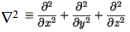
•Laplace'i operaator on matemaatiline teisenduseeskiri, mis seab skalaarsele väljale vastavusse tema teist järku tuletise ruumikoordinaatide järgi.

Kui see tuletis on võrdeline sama välja ajalise tuletisega, tekib lainevõrrand.

Kui elektroodi kujutada ette ∞ tasandina, siis elektrivälja potentsiaal muutub

ainult perpendikulaarselt (ristloodselt) kaugusega plaadist ja saame kirjutada

lihtsustatud kujul, kus x on kaugus elektroodi pinnast (risti pinnaga).

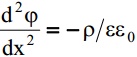
Osakeste jaotus allub Boltzmanni võrrandile

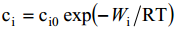
kus c_i0 on i-nda osakese konts. lahuse sisemuses, c_i on osakeste kontsentratsioon kaugusel x elektroodi pinnast, W_i – 1 mooli osakeste lahuse sisemusest elektrilisse kaksikkihti üleviimiseks tehtav töö.

Eeldatakse, et W_i on puhtalt elektrostaatiline töö

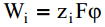
Need tehtud lähendused piiravad aga kahjuks oluliselt Gouy teooria rakendatavust.

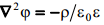
Poissoni võrrand eeldab, et elektriväli on elektrilise kaksikkihi piires pidev ja potentsiaali on võimalik määrata igas välja punktis. Kahjuks ilmneb reaalsetes süsteemides elektrivälja tugevuse ebaühtlus, mis on seotud sellega, et ioonid on mingite kindlate mõõtmetega (mitte punktid). Siit ka põhjus, miks Gouy teooria on rakendatav vaid lahjades lahustes.’

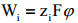
W_i sisaldab peale elektrostaatilise ka teisi jõude, mida Gouy teooria ei arvesta. Ei arvestata spetsiifilist adsorptsiooni põhjustavaid jõude ning tööd, mida tehakse lahusti väljatõrjumiseks elektrilisest kaksikkihist lahuse sisemusse. Ei arvestata ioonide vastastikust toimet, mis on seotud steeriliste faktoritega elektrilises kaksikkihis. Ei arvestata ioonide solvatatsiooni ja solvaatkatete deformatsiooni osakeste sisenemisel elektrilisse kaksikkihti.

Eelnevate võrrandite alusel saame:

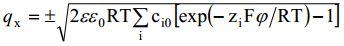
kus märgid ruutjuure ees vastavad olukorrale

Eeldades, et difuusne kiht ulatub välja kuni elektroodi pinnani (x =0, ϕ= ϕ₀ ja q_x = -q), saame elektroodi laengu avaldise:

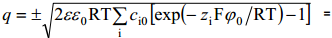
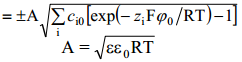
Võrrand sobib suvalise elektrolüütide segu jaoks. Leiame võrrandi 1,1-elektrolüüdi korral: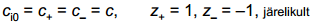

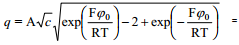
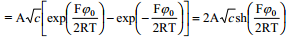
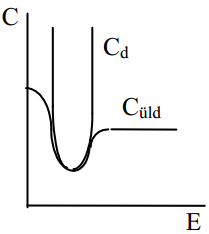
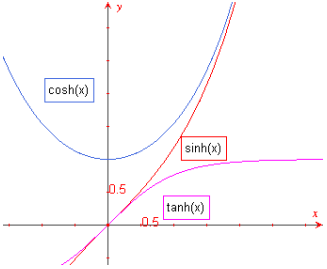
see on difuusse kihi diferentsiaalmahtuvuse sõltuvus elektroodi laengust on paraboolikujuline. C_d on minimaalne kohal E_q=0, sellest punktist kaugenedes C_d kasvab väga kiiresti. Kvalitatiivselt on see kõik kooskõlas eksperimentaalsete tulemustega.

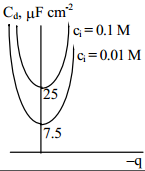
Diferentseerides võrrandi,

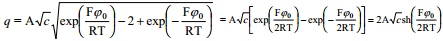
saame difuusse kihi diferentsiaal-mahtuvuse jaoks avaldise

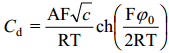
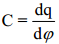
Selleks, et tõlgendada C_d sõltuvust lahuse kontsentratsioonist ja pinnalaengu tihedusest q_M , on mugav kasutada kondensaatori efektiivset paksust λ.

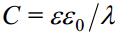
Kasutades eelnevaid võrrandeid, saame:

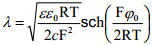
Null-laengu lähedases alas, kus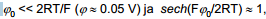

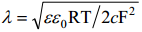
Seega null-laengu lähedases alas võime lõpmatult paksu difusioonikihi asemel vaadelda mingit efektiivse paksusega lõplike mõõtmetega kondensaatorit, mille plaatidevaheline kaugus on võrdne λ.

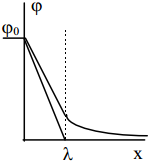λ on võimalik määrata, tuginedes graafikule, mis iseloomustab laengujaotuse sõltuvust kaugusest x.

Eelneva võrrandi analüüs näitab, et λ väheneb, kui lahuse kontsentratsioon kasvab. Teiste sõnadega, difuusset kaksikkihti surutakse kokku, kui kontsentratsioon kasvab, see on difuussus väheneb lahuse kontsentratsiooni kasvades. EKK difuussus kasvab lahuse temperatuuri kasvades, s.o. soojusliikumise intensiivistudes, C_d kasvab samuti ka q_M kasvades, samuti elektrilise kaksikkihi mahtuvus kasvab ka pinnalaengu kasvades.

Et iseloomustada potentsiaali jaotust difuusses kihis, selleks kasutatakse järgnevat võrrandit. Saadakse, et

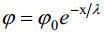
millest järeldub, et väikeste ϕ−de korral on potentsiaalilangus elektrilises kaksikkihis eksponentsiaalne.

Gouy teooria võimaldab kvalitatiivselt iseloomustada paljusid eksperimentaalselt leitud efekte ja leida erinevaid parameetreid, kuidei võimalda selgitada ioonide spetsiifilise adsorptsiooni nähtusi. Selle teooria rakendamisel saadud tulemused erinevad eksperimentaalsetest andmetest tunduvalt:

näit.: 0.01 M NaF lahuses, kui ϕ₀ =1V (E_q=0 suhtes), siis

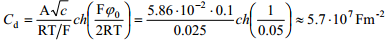
eksperimentaalselt on saadud: C_üld =0.2 Fm^-2, so 8 suurusjärku erinev tulemus. Arvutuslik λ≈1.24⋅10^-8 nm, st 10⁷ korda väiksem kui eksperimentaalne väärtus.

Sellised anomaalsed C_d väärtused on tingitud asjaolust et Gouy teooria vaatleb ioone punktlaengutena, mis võivad ligineda elektroodile kuitahes lähedale, mis tegelikult pole võimalik. Seetõttu annab Helmholtzi teooria oluliselt reaalsemaid C väärtusi, kui Gouy teooria.

Arvestades Helmholtzi teooria ja Gouy teooria positiivseid külgi, tekkis vajadus need ühendada. Seda tegi O. Stern

5. Põhilisi mudelettekujutusi elektrilise kaksikkihi struktuurist - Sterni teooria

Sterni teooria põhiseisukohad:

Ioonide laeng, mis kompenseerib metalli laengu q_M , koosneb kahest osast. Üks osa ioonidest koondub elektroodilähedasse kihti ja moodustab nn. tiheda kihi ehk Helmholtzi kihi. Nende ioonide tsentrid asuvad metalli pinnast keskmiselt kaugusel, mis on võrdne ioonide raadiusega, so x=r. Nende ioonide laeng 1 m² suuruse pinna kohta on võrdne q₁ -ga.

Teine osa ioonidest osaleb soojusliikumises ja moodustab nn. difuusse kihi. Nende ioonide tsentrid asuvad kaugusel x ≥r ja summaarne laeng on q₂.

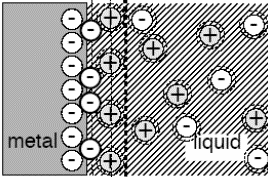
Elektroneutraalsuse tingimus (peab kehtima):

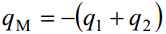
Stern kasutas difuusse kihi laengu arvutamiseks Gouy teooriat, mille põhjal 1,1–elektrolüüdi jaoks (näiteks NaCl):

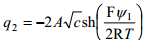q₂ - dif kihi laeng, A – konst, c - lahuse konts

ψ₁ on potentsiaali langus tihedas kihis (muis asju teame, psiid on ainult vaja).

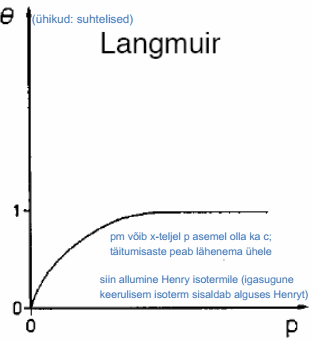
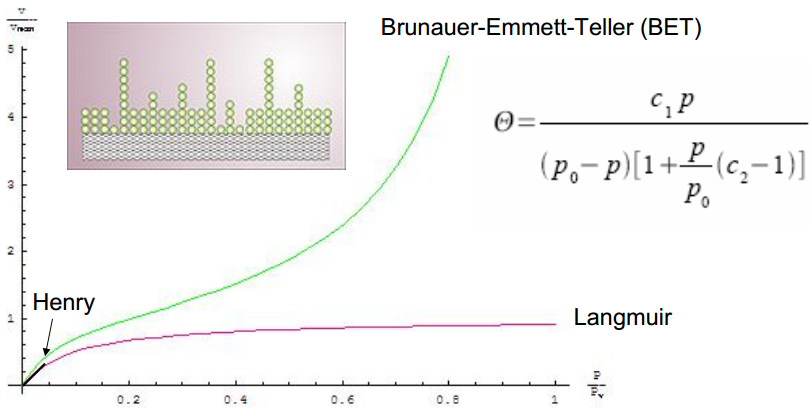
q₁ leidmiseks oletas Stern, et ioonide adsorptsioon allub Langmuiri isotermile ja i-nda osakese toomiseks lahuse sisemusest elektroodi pinna lähedale (kaugusele x = r) tehakse tööd:

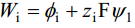(z_i iooni laeng)

φ_i on iooni spetsiifilise adsorptsiooni potentsiaal.

Arvestades, et pinna täitumine ioonidega ei ole suur, võib asemel kasutada Henry isotermi.

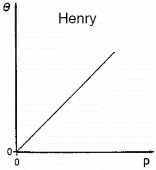Pinnatäitumisaste θ sõltub lineaarselt rõhusr P (Langmuiri isotermi erijuht).

Kui pinna täitumine ioonidega on suur, tuleb kasutada Langmuiri isotermi.

Arvestades Boltzmanni jaotusseadust, saame kaksikkihi tihedas osas olevate ioonide kontsentratsiooni 1,1-elektrolüüdi korral:

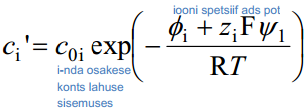tihedas kihis olevate ioonide konts-i arvutamiseks valem

Kui elektroodi pindala on S, siis kaksikkihi ruumala, kus need ioonid paiknevad, on V =2rS ja 1,1-elektrolüüdi jaoks saame laengutiheduse avaldiseks Helmholtzi kihis:

Kasutades Gauss-Ostrogratski teoreemi elektrivälja tugevuse kohta:

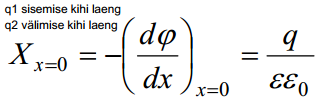elektrivälja tugevus kaugusel x võrdub nulliga e elektroodi pinnal on seotud elektroodi pinna laenguga ja selle süsteemi dieelektrilise läbitavusega; epsilon on elektrolüüdi diel.läbitavus, solvendiks on vesi

ja eeldades, et potentsiaal langeb elektrilise kaksikkihi tihedas osas lineaarselt: (siis on pm võimalikud sellised erijuhud)

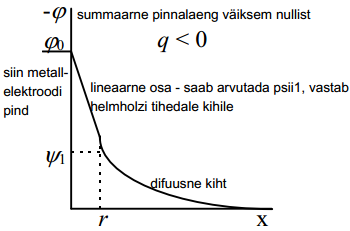
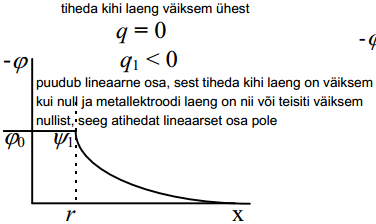
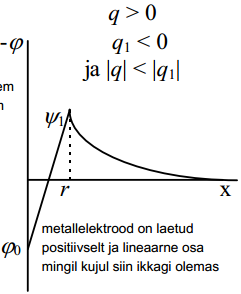
Kasutades Gauss-Ostrogratski teoreemi elektrivälja tugevuse kohta:

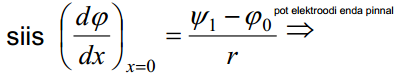
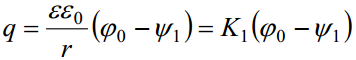
K₁ – elektrilise kaksikkihi integraalmahtuvus, see on elektroodi pinna ja selle vahetus läheduses olevate ioonide poolt moodustatud plaatkondensaatori mahtuvus.

Võrrandite ühendamine annab 1:1-elektrolüüdi jaoks võrrandi:

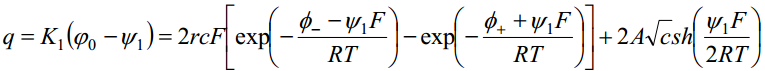
Sterni teooriat kontrollis Frumkin kaastöötajatega. Uuriti elektrilist kaksikkihti pindinaktiivsete elektrolüütide lahustes, kus φ_- = φ₊ = 0. Eelnev võrrand saab sel juhul kuju:

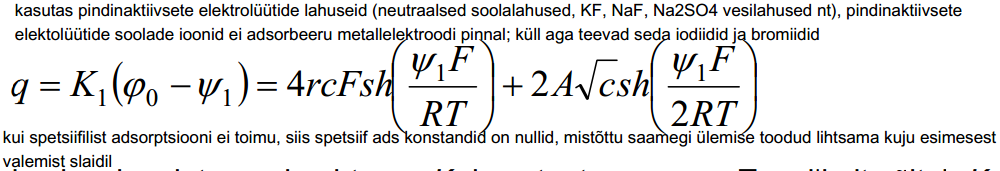
Sterni teooria alusel on integraalmahtuvus K₁ konstantne suurus. Tegelikult sõltub K₁ elektroodi pinnalaengust, sest üleminekulpositiivsetelt pinnalaengutelt negatiivsetele asenduvad anioonid elektrilises kaksikkihis katioonidega ja enamasti on katioonide ning anioonide raadiused erinevad.

Et saada diferentsiaalmahtuvust, eelnev võrrand diferentseeritakse.

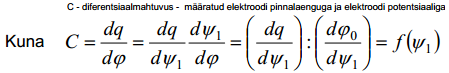
siis f(ψ₁) konkreetse kuju (graafilise) saab leida pärast osaliikmete 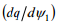ja 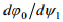leidmist. Esimene on leitav, kui me diferentseerime avaldist, teine aga ϕ₀ avaldise diferentseerimisel:

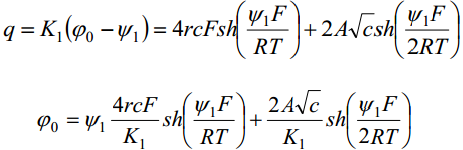saame leida potentsiaalikõvera kuju

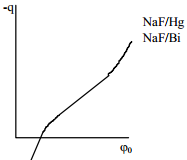
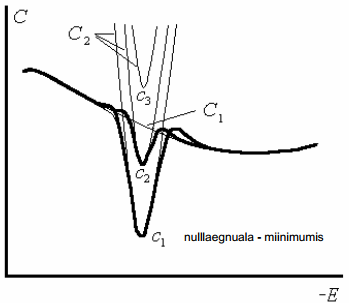
Sterni teooria alusel arvutatud C,ϕ₀ -kõveraid võrreldi eksperimentaalsete kõveratega. Üldiselt on kvalitatiivne kooskõla olemas

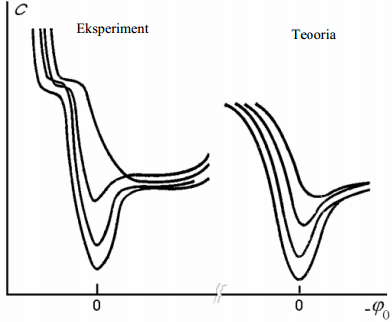reeglina kõverad omavad miinimumi kohal 0 (sellele vastab null-laengu pot: elektroodi summaarne pinnalaeng on null) null-laengu miinimum võib sõltuda elektrolüüdi kontsentratsioonist - ta pole konstant; nt Bi-elektroodil -0,5

Teooria ja eksperimendi erinevused tulenevad:

eksperiment tehti HCl ja KCl vesilahuste s, aga Cl- –ioonid adsorbeeruvad spetsiifiliselt

K₁ ^- ja K₁ ⁺ loeti konstantideks, mida nad tegelikult pole, sest kaksikkihi paksus oleneb osakeste deformatsioonist elektriväljas

kui pole spetsiifiliselt adsorbeeruvaid ioone, siis kõik ülejäänud ioonid peaksid olema võrdväärsed ja asuma kõik difuusses kihis. Järelikult peaks elektrilise kaksikkihi tiheda osa laeng q₁ olema null. Tegelikult Sterni teooria järgi q₁ ≠0, kui φ₊ = φ_- =0

6. Põhilisi mudelettekujutusi elektrilise kaksikkihi struktuurist - Grahame teooria

Grahame eeldas, et kui puudub ioonide spetsiifiline adsorptsioon, q₁=0 ja q=-q₂ (arvestades elektroneutraalsuse printsiipi).

Et seda füüsikaliselt põhjendada, jagas Grahame elektrilise kaksikkihi tiheda osa kaheks (sisemiseks ja välimiseks Helmholzi kihiks).

Spetsiifiliselt adsorbeeruvate ioonide tsentrid asuvad elektroodi pinnast kaugusel x₁, ehk nn sisemisel Helmholtzi tasandil, mille potentsiaal lahuse sisemuse suhtes on ψ_i.

Soojusliikumises osalevad ioonid, mis moodustavad elektrilise kaksikkihi difuusse osa, võivad läheneda elektroodi pinnale kuni kauguseni x₂, so välise Helmholtzi tasandini, mille potentsiaal lahuse sisemuse suhtes on ψ₀.

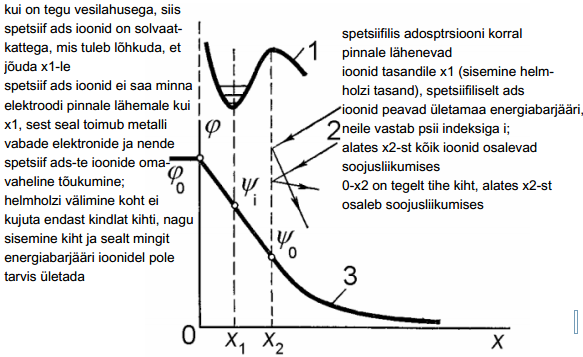
Elektrilise kaksikkihi ehitus Grahame'i mudeli järgi: x₁ – sisemine Helmholtzi tasand, x₂ – väline Helmholtzi tasand, 1 – spets. ads. iooni potentsiaalikõver, 2 - ioonide liikumine difuusses kihis, 3 – potentsiaali muutus kaksikkihis.

Tasandil x₁ asuvad ioonid (spetsiifiliselt adsorbeeruvad ioonid) asuvad nn. potentsiaalse energia miinimumis.

Üleminekul lahusesse peavad nad ületama metalli ja ioonide vahelisest spetsiifilisest toimest tingitud jõu.

Ioonide jõudmiseks Helmholtzi sisemisele tasandile tuleb aga energiat kulutada solvaatkihi osaliseks või täielikuks lõhkumiseks.

Ioonide ja metalli vastastikuse toime ning ioonide ja lahusti omavahelise toime jõudude vahekord määrabki ära ioonide spetsiifilise adsorptsiooni võime. Ioonide liikumist elektroodile lähemale kui x₁ takistab nende elektronkatte ja metalli vabade elektronide omavaheline tõukumine.

Erinevalt sisemisest Helmholtzi tasandist, ei kujuta väline tasand endast ioonide kihti, vaid on mingi mõtteline piir — kaugus elektroodi pinnast, milleni võivad ligineda soojusliikumisesosalevad ioonid. Tasandi x₂ ja lahuse sisemuse vahel pole mingit energeetilist barjääri.

Grahame näitas, et kui puudub osakeste spetsiifiline adsorptsioon, siis on elektriline kaksikkiht ette kujutatav kahe järjestikku lülitatud kondensaatorina.

(nt fluoriidi või sulfaadi lahusega)

fii0 elektroodi potentsiaal; psi0 potentsiaal helmholzi välimisel tasandil

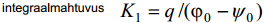
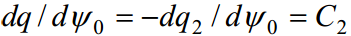
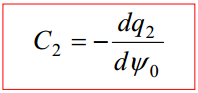
Seega, spetsiifilise adsorptsiooni puudumisel saame:

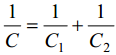C₁ - tiheda kihi osamahtuvus, C₂ - difuusse kihi osamahtuvus

Seega on elektrilise kaksikkihi üldine mahtuvus vaadeldav kahe järjestikku lülitatud kondensaatori mahtuvusena.

Kui aga q₁ ≠0, siis q ≠-q₂ ja eelnev võrrand ei kehti. spetsiifiliselt adsorbeeruvate ioonide korral on siis nii

Teine Grahame eeldus on, et juhul, kui puudub spetsiifiline adsorptsioon, siis sõltub tiheda kihi mahtuvus ainult laengust, mitte kontsentratsioonist:

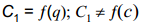
See eeldus võimaldab leida elektrilise kaksikkihi diferentsiaalmahtuvuse kõverad suvalise koostisega lahuses, kui on olemas C,E-kõver ühes suvalises lahuses.

Difuusse kihi jaoks eeldatakse, et kehtib Gouy teooria, seega

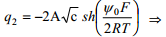
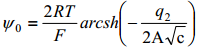
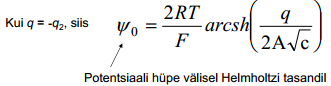kõik muud on konstandid va q ja c (eksperimentaalselt teame elektrolüüdi konts-i ja mõõdame diferentsiaalmahtuvuse, mille kaudu saab summaarse q ka leida)

ning asendades, saame

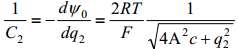
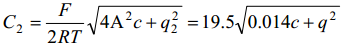
kus konstandid vastavad vesilahusele 25°C juures ja [C₂ ]=Fm^-2, [c] = mool dm^-3 ja [q]=Cm^-2.

1,1-elektrolüüdi korral võib arcsh asendada logaritmilise avaldisega vastavalt seosele:

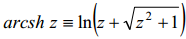
Väikeste laengute korral (väikese z korral arcsh z ≈z) saame ψ₀ lineaarse sõltuvuse laengust:

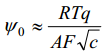psii0 - pot langus helmh välisel tasandil, mida suurem see on, seda suurem ka elektroodi pinnalaeng q e tegu võrdelise sõltuvusega

Suurte laengute korral võib võrrandit lihtsustada: sõltuvalt summaarsest elektroodi pinnalaengust

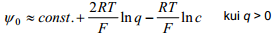
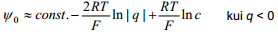
Teoreetiliste kõverate arvutamine ja Grahame'i mudeli kontroll toimub järgmiselt:

võetakse C,E-kõver kõige kontsentreerituma pindinaktiivse lahuse jaoks. Üldjuhul Hg|NaF – 0.9 M NaF kõver (mida suurem elektrolüüdi konts, seda väiksem kõver tuleb)

integreeritakse C,E-kõver, so leitakse q,E-sõltuvus, kuna

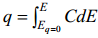C,E-kõver viiakse üle C,q-kõveraks.

leitakse C₂,q-kõver (C₂ leitakse arvutuslikult)

leitakse leitakse tiheda kihi mahtuvus

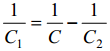
kasutades C₁,q-sõltuvust ja oletades, et C₁ ei sõltu kontsentratsioonist, C₂,q- kõver järgmise elektrolüüdi jaoks.

Leitakse summaarne mahtuvus ja koostatakse uus teoreetiline C,q-kõver.

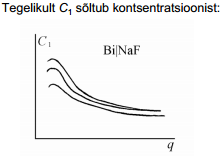
Summaarne mahtuvus on ära määratud väiksema osamahtuvusega, see on null- laengu alas määrab summaarse mahtuvuse difuusse kihi mahtuvus, kui c_el < 0.05 M. Kui |q|> 2.0μCcm^-2, siis juba määrab tiheda kihi mahtuvus.

7. Elektrilise kaksikkihi uurimise meetodid (adsorptsiooniline- ja elektrokapillaarkõverate meetod)

Adsorptsiooniline meetod

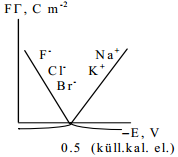
Järgmisel joonisel on kujutatud Na⁺ ja SO₄ ^2- pindliia sõltuvus elektroodi potentsiaalist. saab arvutada nii na kui so4(2-) ioonide gibbsi pindliia Na-ioonid määravad ära null-laengu potsentsiaali (?)

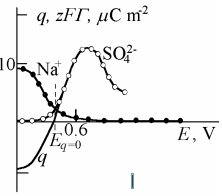
pos pinnalaengud

neg pinnalaengud

nii võib kirjeldada ka teisi erinevaid süsteeme, mitteainult na vesilahust; aga see ads-meetod jäi oma ajale nn jalgu, tänapäeval kasutatakse täpsemaid ja enamlevinumaid meetodeid el.kaksikkihi mõõtmiseks.

Kasutades elektroneutraalsuse põhitingimust (ratsionaalne e suhteline potentsiaal)

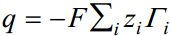
saame leida elektroodi laengu q, E_q=0 ja suhtelise potentsiaali ϕ_o = E – E_q=0.

Elektrokapillaarkõverate meetod (ka ajalooline meetod; jaguneb kaheks erinevaks meetodiks)

Statsionaarse tilga meetod (Hg loigu meetod)

Põhineb tasapinnal asuva vedela metalli tilga kuju uurimisel.

Pindpinevusjõudude mõjul püüab Hg-tilk võtta kera kuju, kuna võrdse ruumalaga kehadest on kera minimaalse pindalaga. Teiselt poolt püüab raskusjõud tilka laiali venitada üle kogu tasapinna. Kahe vastastikku mõjuva jõu tulemusena omandab Hg- tilk ellipsoidaalse kuju. Ellipsi pooltelgede suhtest on arvutatav σ (pindpinevus). Antud meetod annab küll absoluutseid σ-väärtusi, kuid on väga töömahukas ja ebatäpne.

Gouy kapillaarse elektromeetri meetod

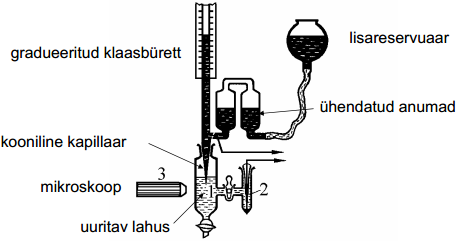
siin asub vedel metall, nt elavhõbe; klaasbürett lõppeb otsast koonusega, koonuse ots on sukeldatud uuritavasse lahusesse; kapillaari otsa võimalik mikroskoobiga uurida; pindpinevusjõud uuritava lahuse ja kapillaari otsa vahel mõjub pindpin.jõud, teisalt raskusjõud, nende vahel valitseb mingi tasakaaluline jõudude vahekord, mis lõpuks püstitub; saame anda potentsiaali peale, siis kindlasti meniski asukoht muutub; elavhõbeda samba kõrgus h on võrdeline pindpinevusjõuga, kontsant k on iga süsteemi jaoks eraldi määratud

Vedel Hg asub gradueeritud klaasbüretis, mis alt lõpeb koonilise kapillaariga. Kapillaari ots on asetatud uuritavasse lahusesse. Piirpind lahuse ja Hg vahel asub kapillaari sees ja tema asukohta on võimalik jälgida spetsiaalse mikroskoobi abil. Pindpinevusjõud püüab meniski asukoha viia üles kapillaari laiemasse ossa, kuid raskusjõud viia alla tagasi. Nende kahe jõu vahekord määrabki ära tasakaalu. Kui nüüd muuta kas ϕvõi koostist, siis muutub meniski asukoht. Kui aga ühendatud anumate ja lisareservuaari abil hoida meniski asukoht konstantne, siis Hg samba kõrgus h on võrdeline σ-ga.

kusjuures k määratakse eraldi iga süsteemi korral standardses elektrolüüdi lahuses (NaHSO₄), mille jaoks σ absoluutväärtused on määratud loigumeetodil.

Nagu eelpool näidatud, on vastavalt Helmholtzi teooriale elektronkapillaarkõver (tagurpidi pööratud parabool, maksimum=nulllaengupotentsiaal) ümberpööratud parabooli kujuline. Kvalitatiivselt võib sellise kujuga kõverat kirjeldada ka sellega, et samanimeliste ioonide tõukumine on seda suurem, mida suurem on pinnalaeng (q). Suurem tõukumine aga tähendab tööd mida on vaja teha elektroodi pinna suurendamiseks, seega ka σ väheneb (seetõttu on pööratud parabool).

Elektronkapillaarkõvera võrrandi lihtsustamisel saame Lippmanni võrrandi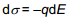

Võrrandi saab teisendada kujule

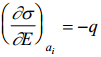
Seega elektronkapillaarkõvera tõus annab meile pinnalaengu. Kõvera maksimumpunktis ∂σ/∂E=0 ja q= 0. Seega elektronkapillaarkõvera maksimumile vastab null-laengupotentsiaal.

Teiselt poolt Lippmanni võrrandi ja elektroneutraalsuse tingimustes binaarse elektrolüüdi korral saame:

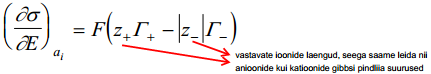
Peale teisendusi saame leida anioonide ja katioonide pindliiad ehk Gibbsi adsorptsiooni. Kui aga neutraalse elektrolüüdi foonil (pindinaktiine elektrolüüdi lahus) varieerida orgaanilise ühendi aktiivsust, siis:

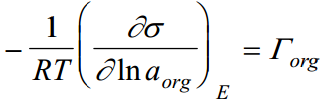a - nat.log org ünedi aktiivsusest, saame leida org ühendi gibbsi pindliia väärtuse, kuid ka muid erinevaid suurusi

Seega elektrokapillaaria meetod võimaldab leida q, E_q=0 , Γ_i ja Γ_org.

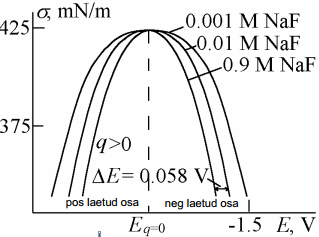
Elektrokapillaarkõvera kuju sõltub pindinaktiivse elektrolüüdi kontsentratsioonist ja tüübist:

siin toodud elektrokapillaarkõverad kolme kuju sõltub pindinaktiivse aine kontsentratsioonist (mida kontsentreeritum, seda teravam kõver) ja ka tüübist null-laengu pot ei sõltu kontsentratsioonist, vaid on konst

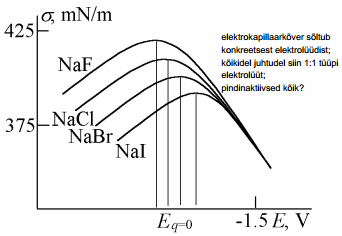
mc MNaJ+ (1-m)c MNaF (lähtudes sellest võrrandist- igasuguste kontsentratsioonide korral on tegu konst ioonse jõuga, kus tuleb sobivas vahekorras pindinaktiivne ja pindaktiivne aine)

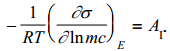m - pindaktiivse aine konts (nt NaI), c- pindinaktiivse komponendi e naf konts, võrrandist leiame aniooni pindkonts väärtusi

A_i – aniooni pindkontsentratsioon

Elektrokapillaarkõverad orgaanilist ühendit sisaldavas lahuses:

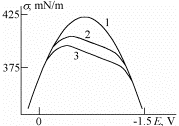1 – 0.5M Na2 SO4

2 –0.1M normaalbutanooli lisand

3 – 0.2M normaalbutanooli lisand

mida rohkem orgaanikat seda rohkem paremale kõvera max nihkub; kas orgaaniline molekul adsorbeerub pos või neg poolega? null-laengu nihe positiivne e org molekul adsorbeerus elektroodi pinnale rohkem positiivselt polariseeritud osaga.

0,1 ja 0,2 M lahuse kohta: org üh. lisandiga elektrokapillaarkõverad - kui lisame org ühendeid, siis pindpinevus alaneb ja see alanemine seda suurem, mida rohkem on org ühendit

Pindpinevuse alanemine on tingitud sellest, pindliig Hg elektroodil on positiivne. Suurte negatiivsete ja positiivsete potentsiaalide (need pot, kus elektrokapillaarkõver hakkab lõikuma potentsiaaliteljega) juures toimub org. aine desorptsioon, kuna kondensaator tõmbab elektrilisse kaksikkihti selle dielektriku, mille ε on suurem

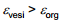
Antud juhul toimub E_q=0 nihe positiivses suunas, mida seletatakse sellega, et orgaanilise aine molekul on pinnal positiivse otsaga. E_q=0 võib nihkuda ka negatiivses suunas.

8. Elektrilise kaksikkihi uurimise meetodid (impedantsi- ehk vahelduvvoolusilla meetod)

Elektriline kaksikkiht (EKK) on vaadeldav tasaparalleelse kondensaatorina. Nn. ideaalselt polariseeritavate elektroodidekorral (elektroodid, millel ei toimu elektrokeemilised reaktsioonid, kogu väljastpoolt antav laeng kulutatakse ainult elektroodi potentsiaali muutmiseks, elektrilise kaksikkihi laadimiseks) on elektrilise kaksikkihi mahtuvust võimalik eksperimentaalselt määrata.

Kui elektrood ei ole ideaalselt polariseeritav, siis osa laengust (ja voolust ja ka mahtuvusest) kulub elektrokeemilisele reaktsioonile.

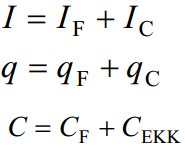kaks komponenti, kuna süsteemid pole kunagi ideaalsed; faraday komponent tingitud kõrvalekalletest, teie osa on ideaalne mahtuvuslik komponent mahtuvus on määratud faraday ja tõelise mahtuvusliku elektrilise kaksikkihi komponendiga.

EKK mahtuvuse mõõtmine seisneb selles, et elektroodile antakse väike laeng Δq, mis kutsub esile potentsiaalimuutuse ΔE.

Δq/ΔE ≈dq/dE = C

Suurust Δq/ΔE nim. polarisatsiooniliseks mahtuvuseks.

Mahtuvust võib mõõta mitmeti, kuid kõige täpsemaks meetodiks on impedantsi- ehk vahelduvvoolusilla meetod.

Tähistame elektrokeemilises reaktsioonis osaleva i-nda osakese pindkontsentratsiooni A_i.

Süsteemi läbiv vool sõltub pindkontsentratsioonist I_F = ƒ(A_i; ϕ), ⇒A_i =ƒ₁ (I_F; ϕ). Elektrokeemilise reaktsiooni komponent e Faraday komponent, funtksioon koosneb kahest osast.

Seega, kui C_EKK ei ole ainult funktsioon ϕ-st vaid ka A_i-st (näiteks spetsiifilise adsorptsiooni korral), siis

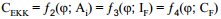
Kuna C_F ja C_EKK on omavahel seotud, siis selline mahtuvuse lahutamine mahtuvuslikuks ja Faraday komponendiks on väga tinglik.

Sageli kasutatakse nende kahe komponendi eraldamiseks C sõltuvust vahelduvvoolu sagedusest ν. Kuna kõrgetel sagedustel ei jõua elektrokeemiliselt aktiivne aine elektroodi pinnale difundeeruda (ν≥1000…10000 Hz), siis jääb järele ainult C_EKK. Komponentide omavahelise sõltuvuse tõttu on selline lähend õige muidugi ainult esimeses lähenduses.

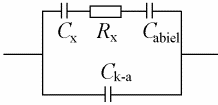Elektrokeemiline süsteem koosneb kolmest mahtuvusest: C_x – uuritava elektroodi EKK mahtuvus; C_abiel – abielektroodi EKK mahtuvus; C_k-a – katood-anood-süsteemi mahtuvus (R_x – lahuse ehk elektrolüüdi takistus, mõnikord tähistatakse R_el või R_s ).

Kuna uuritava ja võrdluselektroodi mahtuvused on järjestikku, siis nende summaarne mahtuvus:

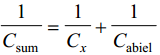
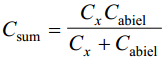
C_abiel ellimineeritakse sellega, et tööelektroodi polariseerimiseks kasutatakse tavaliselt suurepinnalist Pt-elektroodi (Pt-võrk) ja seega C_abiel >>C_x ja (C_abiel )^-1<< (C_x )^-1 ja abielektroodi mahtuvuse võib jätta arvestamata. Mõningatel juhtudel võib tööelektroodina kasutada suurepinnalist süsinikelektroodi.

katoodi ja anoodi vaheline kaugus on oluliselt suurem kui ekk paksus ja seega võime süsteemi lihtsustada ja võtta ära C (katood-anood), mistõttu jääb järele ainult Cx ja Rx ja neid kahte komponenti on meil vaja teada

Kogu süsteemi mahtuvus: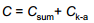

Plaatkondensaatori mahtuvus C = εε₀ /d. Kuna anoodi ja katoodi vaheline kaugus on palju suurem elektrilise kaksikkihi paksusest, siis on C_k-a << C_x , ⇒võime süsteemi iseloomustada lihtsustatud skeemiga

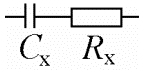
Sellise ahela jaoks võib kirjutada seose

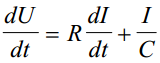
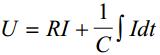potentsuaal U on määratud IR'ga ja viimase osaga, mis arvestab süsteemi mahtuvust; need kaks võrrandit võiksid olla kõikide ekk mahtuvuste määramise alusteks; nendest valemitest saame Rx ja Cx'i abil kõige täpsemad tulemused saame vahelduvvoolu silla abil e impedantsi abil

Eelmised kaks võrrandit on kõigi EKK mahtuvuse määramise meetodite aluseks. Eksperimendi printsiip seisneb selles, et tekitatakse süsteemis potentsiaalilangus ning jälgitakse voolu muutust ajas või programmeeritakse voolu muutus ja jälgitakse potentsiaali sõltuvust ajas. Seejärel leitakse valemite abil R ja C.

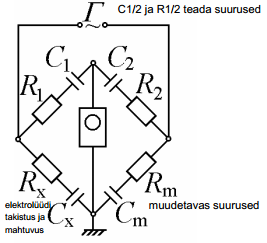kui anda signaaligeneraatorist otstele signaal ja veel lisada ostsillograaf, siis saab varieerides Cm ja Rm väärtusi, saab viia silla tasakaalu nii, et neil on võimalik määrata Rx ja Cx (kui tasakaal, siis on kriips, muidu sinusiodaalne)

silla ahela otstele anname muutuva amplituudiga vahelduvvoolu, mille voolutugevus teada(sinusoidaalne); näeme, et voolu ja pinge vahel on faasinihe (vt järgmine slaid)

Ahela otsetele rakendatakse muutuva amplituudiga vahelduvvool (voolutugevusega I0), mille nurksagedus ω=2πν ja faasinihe on α.

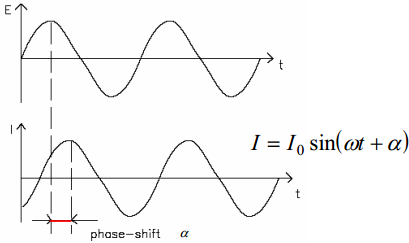
Takisti Rx = Z’(ω)

Kondensaator 1/jC_xω= Z”(ω)

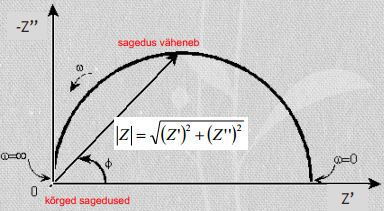
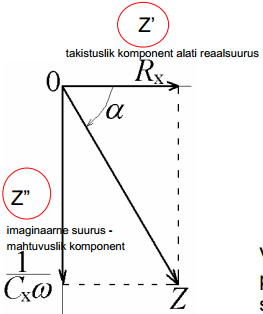- faasinihe, võib olla nii pos kui ka neg suurus, võib olla -90st kuni +90ni; kui faasinihe on 0 (Rx teljel), siis on tegu puhta takistusliku komponendiga, kui faasinihe on -90 (Z"), siis on puhas mahtuvuslik komponent, kui 0 ja -90 vahel, siis on tegu segakineetikaga; induktorite puhul faasinihe +90; reaalsetes elektrokeemilistest süsteemides, seal ilmselt mingit induktiivsust ei ole, kui meil pole väga spetsiif süsteem

kui ahela otstele rakendame voolu, siis graafik sinusoidaalne ja sellele vastavalt võib kirjutada pinge U jaoks alltoodud avaldise; näeme, et elektrokeemiline ahel avaldab pot muutusele teatud takistus ja see summaarne suurus on jagatav kaheks osaks, summaarselt on Z komplekstakistus

kompleksimpedantsi Z kaudu saame alati leida nii takistusliku kui mahtuvusliku komponenti (Pythagoras), lisaks ka faasinikhke

Sellele vastavalt

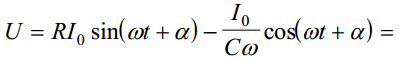
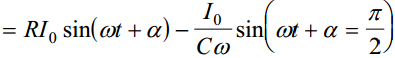
Võrrandist ilmneb, et elektrokeemiline ahel avaldab potentsiaalimuutusele teatud takistust. Sellise süsteemi summaarne takistus on avaldatav kui kompleksmuutus ja funktsioon Z on nn. elektrokeemiline impedants:

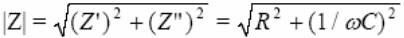
kus R on aktiivtakistus ja j/Cω on reaktiivtakistus ning j = sqrt(−1)

Ahela otsetele rakendatakse muutuva amplituudiga vahelduvvool (voolutugevusega I₀), mille nurksagedus ω=2πν ja faasinihe on α.

Silla tasakaaluolekus: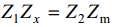

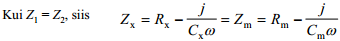
⇒R_x = R_m ja C_x = C_m ja vahelduvvoolusilla abil on võimalik mõõta EKK tõelisi mahtuvusi.

ekk vaadeldav kui tasaparalleelne kondekas; ekk omadused sõltuvad aga väga oluliselt elektroodi pinnalaengust, sest ekk ehitus pinnalaengu muutudes muutub, lisaks muutuvad mõõtmed, diel omadused, lahusti võib kemosorbeeruda, anioonid-katioonid võivad ...

olemdas integraal- ja diferentsiaalmahtuvused

Eelnevalt vaatlesime, et esimeses väga jämedas lähenduses on EKK vaadeldav tasaparalleelse kondensaatorina, kuid erinevalt tavalisest elektrilisest kondensaatorist sõltuvad EKK dielektrilised omadused pinnalaengust, kuna EKK ehitus muutub (lahusti kemosorptsioon, anioonide ja katioonide erinev hüdratatsioon jm.) ning seega muutuvad ka EKK mõõtmed ning dielektrilised omadused. Seetõttu tuleb eristada diferentsiaalset

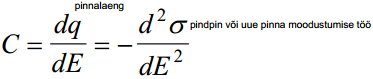potentsiaal on alati teada, mõõdame mahtuvuse -> saame pinnalaengu ja pindpinevuse

ning integraalset mahtuvust

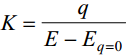suhteline ehk ratsionaalpotentsiaal - pot miinus null-laengu pit

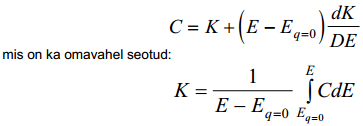
C ja K langevad kokku, kui E=E_q=0 või kui K ei sõltu E-st.

Vahelduvvoolusilla abil mõõdetakse elektroodi pinnalaengu muutuse Δq sõltuvust ΔE-st. Selleks, et mahtuvuse võiks mingi keskmise potentsiaali jaoks konstantseks lugeda, võetakse ΔE võimalikult väike (1…5 mV). Seega mõõdetakse selle meetodiga diferentsiaalmahtuvust. EKK integraalmahtuvust võib arvutada võrrandi

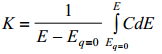seega impedantsi sild mõõdab meil diferentsiaalmahtuvuse (see huvipakkuvam, kuigi saab ka arvutada integraalmahtuvuse)

Vaheetapina saadakse q,E-sõltuvused, mis on C,E-kõvera alla jääv pindala:

Diferentsiaalmahtuvuse suuremad väärtused q>0 korral on tingitud sellest, et anioonide solvatatsioonienergia on väiksem ja elektriväljas toimub aniooni desolvatatsioon ja EKK efektiivne paksus väheneb. E_q=0 lähedases alas aga E väheneb ning soojusliikumine viib EKK mõõtmete kasvule, moodustub difuusne kiht.

9. Poorsed materjalid ja nende karakteriseerimine. Brunauer-Emmett-Telleri, XRD, Raman spektroskoopia, SEM ja TEM meetodid

BET

SEM

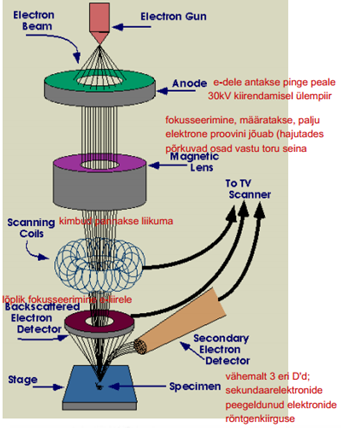SEM tööpõhimõte – põhineb objekti pinna skaneerimisel kõrge energiaga fokuseeritud elektronkimbuga (/sondiga). Elektronide interaktsioonil prooviga saadakse infot tema pinna topograafia, koostise ja teiste omaduste (nt elektrijuhtivuse, lokaalsete väljade jm.) kohta. Sõltuvalt mikroskoobist on võimalik detekteerida erinevaid singaale. Tüüpilised signaalid, mida detekteeritakse on sekundaarsed elektronid, hajunud elektronid, karakteristlik x-ray, elektron-magnetkiirgus (katoodluminestsents), proovi vool, läbivad elektronid õhukeste proovide korral

Elektronkahur - eesmärgiks tekitada stabiilset elektronkiirt reguleeritava energiaga. SEMis kasutatav pingete vahemik on 0,1-40 kV. W hõõgniiti kuumutatakse u 2500 kraadini, sest seal on e^- -de emissioon stabiilne. Filament on ümbritsetud silindrilise kattega (Wehnelt), millel on negatiivne potentsiaal hõõgniidi suhtes. Katte avast väljub filamendilt väljunud e^- -de kiir, mis hajub teatud nurga all. Need e^- -d kiirendatakse anoodi (ja objekti) suunas viimaste positiivsete potentsiaali tõttu. Filamendi ja anoodi vahelist kiirendavat pinget saab muuta vahemikus 0,1-30 kV

Kondensorläätsi kasutatakse elektronkiire koondamiseks. Need on spetsiaalse mähised (elektromagnetilised läätsed) elektronkiire kanali ümber (topeltläätsesüsteem tavaliselt). P –poolusking, C – mähised (coils). Läätse läbiva voolu tugevuse muutmisega muudetakse magnetvälja tugevust kiirekanalis ja sellega muudetakse elektronkiire hajumisnurka, tehes kiire kitsamaks või laiemaks ning koos sellega kas suurendakase või vähendatakse voolu.

Kui primaarelektronide kiir interakteerub prooviga:

e^--id kaotavad energiat (elastne hajumine, mitteelastne hajumine, elektromagnetkiirgus) proovi tilgakujulises ruumalas (alla 100 nm kuni 5 µm pinnast).

Sisenemissügavus oleneb primaarelektronide energiast, proovi aatomite aatomnumbritest ning proovi tihedusest.

Seega primaarelektronid interakteeruvad proovi aatomitega ja need interaktsioonid produtseerivad signaale (SEM-is eelkõige huvipakkuvad sekundaarelektronid ja peegeldunud elektronid, kuid ka karakteristlik röntgenkiirgus ja proovi läbinud transmissioon-elektronid ning katoodiluminestsents),

Sekundaarelektronide detektorid on pea igas SEM-is, kuid olenevalt masinast ja vajadusest saab juurde lisada ka teisi signaale registreerivad detektorid.

Saadav info: proovi pinna topograafia, koostise ja ka nt elektrilise juhtivuse kohta.

XRD

Braggi võrrandist: mõõtes ära θ ja teades lainepikkust, saame kindlaks teha d ja seeläbi identifitseerida kristallsturktuuri. Kindlad aatomid mõjutavad difrageerunud kiire faasi ja mitte sarnased aatomid kindlates positsioonides võivad põhjustada kindlate difraktsioonipiikide puudumist. On olemas suur andmebaas erinevate difraktsioonimustritega, mis lubab enamikku ühendeid identifitseerida vastavalt difraktsiooni asukohtadele ja intensiivsustele

Meetod baseerub röntgenkiirguse difraktsioonil ning on klassikaline meetod ainete struktuuri määramiseks

Difraktsioon toimu aatomtasanditelt

Meetodi toimimiseks on vaja korrapära – saab uurida vaid kristallilisi aineid

Proove lahustada pole vaja

Braggi võrrand: sinθ=nλ/2d

n-naturaalarv

λ – lainepikkus

d – kristallivõr tasandite vaheline kaugus

θ – langeva ja haijuva kiire vaheline nurk

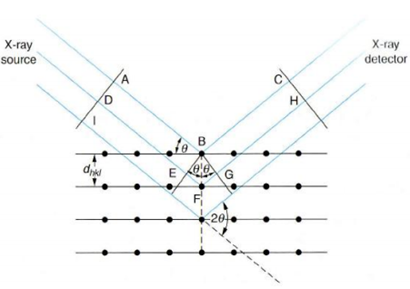
pealelangev kiirgus on monokromaatne

kristallis saab leida palju tasandeid erinevate vahekaugustega (erinevate d-dega)

igale tasandile vastab difraktsioonimaksimum

neid on seda rohkem, mida keerukama ehitusega on kristall

eriti palju on orgaanilistes ainetes

proov enamasti pulbristatakse, vahel saab ka otse pinnalt analüüsi teha

kuna enamik süsinimmaterjale on polükristallilised, siis sobib XRD nende iseloomustamiseks hästi

Raman

Raman spektroskoopia tegeleb valguse mitteelastse hajumise mõõtmisega.

Valguse mitteelastne hajumine on väga väikese intensiivsusega, mis nõuab kõrge tundlikkusega detektorite kasutamist ja suure intensiivsusega monokromaatset valgusallikat.

Tegu on väga hea meetodiga iseloomustamaks kristallilist, nanokristallilist ja amorfset süsinikmaterjali

Raman hajumine

Umbes 1 hajunud kvant 10000000 hajunud kvandi kohta hajub mitte-elastselt

See tähendab, et hajunud kvandi sagedus on erinev pealelangenud kvandi sagedusest

Enamasti on hajunud kvandi sagedus (ja seega ka energia) madalam

Sellist hajumist nimetatakse Raman hajumiseks

Raman hajumise intensiivsus on väga madal!

Energia erinevus võib salvestuda vibratsioonilise, rotatsioonilise või elektroonse energiana

Meie tegeleme ainult vibratsioonilise Raman efektiga

Raman hajumise olemus

Lihtsustatult:

Kvant ergastab molekuli virtuaalsele energianivoole

Enamasti nähtava kiirguse laineala kvandid

Molekul relakseerub tagasi sama elektroonse energianivoo mõnele teisele vibratsiooni-alamnivoole

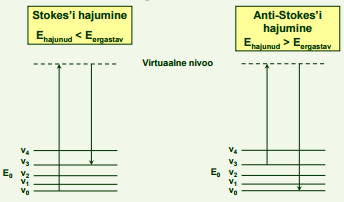
Kuna tavalisel temperatuuril on rõhuv enamus molekule olekus v₀ , siis on rõhuv enamus hajunud kvante Stokes’i kvandid

Raman ergastamine

Ergastamiseks kasutatakse nähtavat valgust või lähiinfrapunast kiirgust

Ergastusenergia on elektroonse ergastuse suurusjärgus

Ergastav kiirgus:

peab olema nii monokromaatne kui võimalik

peab olema piisavalt intensiivne

lainepikkuse muutmise võimalus pole oluline

Seega ideaalne allikas – Laser

Raman spekter

Infona saadakse vibratsioonspekter

Seega, tegemist on vibratsioonspektroskoopiaga nähtavas spektrialas

Vibratsiooninivood on samad, mis IR spektroskoopias

Seetõttu Raman ja IR spektrites joonte asukohad samad

Mitmed IR spektroskoopia puudused ei avaldu

Lahustite puudust pole

Optiliseks materjaliks sobib klaas

Raman spektri x-telg

Raman spektri X teljel pole kiirguskvanti iseloomustav absoluutne suurus vaid kahe kvandi energiate erinevus

Meenutuseks, IR spektris on X teljel võimalik kasutada nii lainepikkust kui ka lainearvu

Raman spektrijoone tekketingimus

Raman spektris on lubatud sellised jooned, mis vastavad võnkumistele, mille käigus muutub molekuli polariseeritavus

vastavate võnkumiste kohta öeldakse, et nad on Raman spektris aktiivsed

Meetod sobib praktiliselt mistahes olekus proovidele: lahused, pulbrid, tahked ained, pastad, geelid jmt

Tahkiste pastade jms korral saadakse spekter pinnalt

TEM

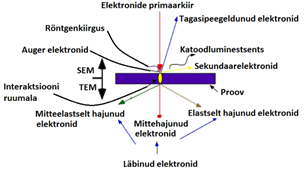
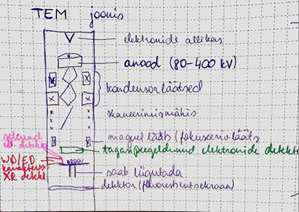
Elektronide genereerimine toimub elektronkahuris, elektronide kiirendamine anoodi abil, elektronkiirega manipuleerimine kondensorsüsteemis. Objektil kogu uuritava ala valgustamine elektronidega. Prooviobjekti saab liigutada, et valida õige koht analüüsiks. Suurendamine toimub mitmete läätsede abi ning suurendatud kujutis kuvatakse fluorestsentseksraanil. Kergete elementide jaoks ei saa kasutada 400 keV, pigem 80-200 keV.

üks võimsamaid materjalide mikro- ja nanoskaalas uurimise vahendeid

võimaldades saavutada aatom-lahutust,

uurida õhukeste objektide struktuurseid omadusi,

elementset ja keemilist koostist ning teisi füüsikalis-keemilisi omadusi suure lokaalsusega.

Oluline TEM puhul see, et kui uurime mingit objekti, siis me ei saa uurida ühte aatomit, vaid peab olema terve aatomite rida üksteise taga, muidu me seda ei näe.

Kaasaegne seade on sageli kõrg-(puhta) vaakumiga nii elektron-optilises kui uurimisobjekti kambris, elektroonse kujutise registreerimisega, objekti 3D manipuleerimisega (nihutamine, keeramine, kallutamine mitme telje ümber) ning varustatud mitmekülgse analüütilise seadmestikuga.

Samuti saab sageli objekti kuumutada kuni või üle 1000 K ja/või jahutada krügeensetele temperatuuridele.

Näiteks alumiiniumsulam, kus 200 kraadi juures hakkab ümberkristalluma, TEMiga saab uurida kuidas see toimub.

Objektid peavad oleva niivõrd õhukesed, et sondi elektronid läbiksid objekti põhiliselt energiakadudeta,

TEM tööpõhimõte

Elektronide allikas asub mikroskoobi ülaosas. Allikast väljunud elektrone kiirendatakse pinge abil. Pinge valitakse vastavalt uuritava objekti materjalile, selle paksusele ja millist informatsiooni soovitakse saada. Kõrge energiaga (kuni 3MeV) mikroskoobid on viimasel ajal haruldasemaks jäänud, kuna madala energiaga mikroskoopide lahutusvõime on märgatavalt paranenud. See on tingitud parematest läätsesüsteemidest ja kvaliteetsemast proovi ettevalmistamisest. Lisaks sellele on leiutatud emissiooni kahurid, mis võimaldavad tekitada elektronkiirt, mille läbimõõt on 1 nm suurusjärgus. Elektronkahuri all on kondensorsüsteem, mis koosneb vähemalt kahest kondensorläätsest. Selle abil on võimalik manipuleerida elektronkiirega, muutes näiteks selle läbimõõtu, mis interakteerub prooviga.

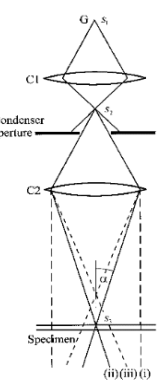Kahe kondensorläätsega sõsteemi korral kiire läbimõõt s1 muudetakse kondensorläätse C1 abil suuruseks s2. Teine kondensorlääts on kasutusel kiire fokuseerimiseks. Ta võib ka muuta kiirt suuruseks s3. (i), (ii), (iii) näitavad seejuures alafokuseeritud, fokuseeritud ja ülefokuseeritud kiiri. Koondumisnurka α saab muuta kondenserapertuuri abil.

Proovikamber asub kondensorsüsteemi all. See on mikroskoobi kõige olulisem osa, kuna väga väikest prooviobjekti tuleb hoida väga täpselt õiges kohas. Seda teostatakse spetsiaalse hoidja abil. Samuti peab olema võimalik seda liigutada mitmeid millimeetreid ja kallutada suurte nurkade all. Kui on vajadus analüüsi järele, siis peab olema lubatud ka röntgenkiirguse pääsemine prooviobjektilt detektorisse. Mõnel juhul on vajalik ka objekti hoidmine väga madalatel või siis teinekord väga kõrgetel (kuni 1000 ^oC). Ka selle jaoks on olemas spetsiaalsed hoidjad. Objektihoidjal objekti vahetamine on lihtne ja kiire, kuna proovi fikseeritakse ühe klambriga ja hoidja saab seadmesse paigaldada läbi lüüsisüsteemi, mis vajab vaid paar minutit pumpamise aega. Reeglina on objekti maksimaalne diameeter 3 mm.

Loeng: Nanopoorse süsiniku saamine (lähteained, meetodid, kloreerimismeetod) ja selle pinna modifitseerimise võimalustest. De Levie mudel

Nanopoorse süsiniku saamise meetodid:

Keemilise aurustus-sadestus meetodil

Orgaaniliste ühendite lagunemisel

Erinevate karbiidide selektiivsel söövitamisel

Orgaaniliste ühendite lagunemisel

Süsinikurikaste orgaaniliste lähteainete kuumutamine (karboniseerimine, pürolüüs) inertatmosfääris (kuumutamisjärgne materjali edasine töötlus tagab soovitud tulemuse saamise)

Lähtematerjalid

Naturaalsed: kookoskoor, puit, tõrv, süsi

Sünteetilised polümeerid

Osasid saadud süsinikke aktiveeritakse pürolüüsi järgselt – nn aktiveeritud süsinikud /Jänese materjalist samade järgnevate punktide kohta: selektiivseks oksüdatsiooniks kasutatakse CO₂, veeauru või KOH

Avab suletud poorid – eripind kasvab

Pikemal oksüdeerimisel poori keskmine suurus kasvab

Füüsikaline aktiveerimine CO₂ või veeauruga >250 °C

Keemiline aktiveerimine – enne karboniseerimist lisatakse lähteainele hapet, tugevat alust või soola (H₃PO₄, KOH, NaOH, CaCl₂, ZnCl₂). Karboniseerimine toimub nii madalamal temperatuuril ja kiiremini, koos samaaegse aktiveerimisega

Saadud süsinikmaterjalil on võrdlemisi lai poorijaotus

Erinevate karbiidide selektiivsel söövitamisel (mitu eri meetodit selleks)

CDC eelised:

CDC on kitsama poorijaotusega kui orgaanilisest materjalist sünteesitud süsinik

CDC säilitab lähtekarbiidi kuju (produkt väga kontrollitud omadustega)

CDC struktuur sõtlub paljudest teguritest:

Lähtekarbiidist (ränikarbiidiga saadakse hästi mikropoorne c-materjal, kuna Si aatomid väikesed + see on kõige odavam lähtekarbiid; Mo₂C aga praktiliselt ainult mesopoorne)

Sünteesi temperatuurist

Termodünaamiliste arvutuste kohaselt võib karbiidist süsiniku sünteesimisel eristada kolme temperatuuri piirkonda: 1. madalatemperatuurne piirkond – CDCd ei teki, kuna termodünaamiliselt on elistatud CCl4 eraldumine 2. Kesktemperatuurne piirkond – tekivad nii CDC kui ka CCl4. Temperatuuri tõstmine viib suurema CDC saagiseni 3. Kõrgtemperatuurne piirkond – ei eki CCl4. Kogu süsinik jääb CDC kujule

Katalüsaatoritest (levinud d-met kloriidid, mida lisatakse karbiidi hulka enne kloreerimist; kalatüsaator suurendab saadud c-materjali grafiitsust, st madalamal T-l saame katalüsaatoriga grafiitsema materjali kui ilma katalüsaatorita (levinumad Fe, Co, Ni karbiidid), peab vaatama, et lähtekloori hulk oleks välja arvutatud ja teada, et ei tekiks ohtu, et saame liiga amorfse/grafitiseerunud materjali Mo karbiidist (kuna see hakkab ka katalüsaatorina tööle üks hetk))

Järeltöötlusest (järeltöötlus süsinikdioksiidiga või veeauruga, et saada suuremat poorsust;)

C sünteesiks võib kasutada erinevaid karbiide:

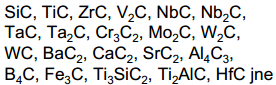
Kui nt lähteaine on Cr₂C₃, siis kroomkloriidid on tahked ained ega taha ka vesiniku töötlemisel produktist eemalduda - esineb probleeme puhta süsiniku saamisel.

A. Halogeenimismeetod (eesmärk võtta C-metall võrgustikust metall välja)

Selektiivne metalliaatomite välja söövitamine karbiidi struktuurist kõrgel temperatuuril (>600°C) ning normaalrõhul

Keemiline reaktsioon: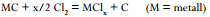

O₂-vabas keskkonnas

MCl_x juhitakse süsteemist välja

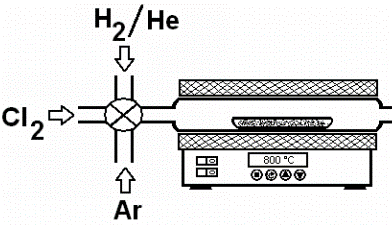Proov puhastatakse Cl₂ ja MCl_x jääkidest:

Intertgaasi voolus

Kuumutades H₂ käes

H₂ kasutatakse poorsuse avamiseks ja pooride suuremaks söövitamiseks

Reaktsiooni viiakse läbi ka teiste halogeenide (peamiselt F₂) ja halogeenhapetega (HF, HCl)

Kloreerimine kõige soodsam ja suuremas skaalas teostatav meetod

karbiide võib ka keemiliselt lagundada toimub kõrgemal T-l kui klooriga töötlemisel (u 300 kraadi), seega see mugavam termilisest lagundamisest soovitud kodus lähtekarbiid panna toruahju (pildil), juhtida torust läbi Ar-i veendumaks, et hapnik välja läinud (muidu saab oksokarbiidi ega saa õiget poorsust), siis tuleb tõsta T soovitud näiduni, nt 800 kraadi, ja avame kraani, nii et toruahju läheb kloor (vajamineva kloori kogus eelnevalt väljaarvutatud, ülekloreerimisel kõrgel T-l võib tekkida oht, et liiga väiksed tekkivad poorid hakkavad üleklorieerimisel suurenema, siis saame materjali, mille poorsust on kunstlikult tõstetud), pärast kloreerimist juhitakse süsteemile uuesti peale Ar, süsteem maha jahutada, seejärel saagis kaaluda, uuesti ahju panna, juhtida Ar läbi, tõsta T 800 kraadini ja juhtida puhastamiseks ahju molekulaarset vesinikku, siis juhime uuesti Ar peale, jahutame süst-i Ar-kk-s maha, nüüd peaks puhas produkt valmis olema

B. Hüdrotermiline karbiidide söövitamine:

Karbiidi reaktsioon superkriitilise veega:

Vesi temperatuuril ja rõhul kriitilisest punktist üleval

T_c ~ 647 K = 374 ^oC

P_c ~ 22 Mpa = ~ 220 atm

Suure reageerimisvõimega ja madala viskoossusega

Reaktsiooni produktid: C, MeO_x, CH₄, CO₂, CO, H₂

H2O:SiC suhe:

Madala suhtega C ja SiO2 sadenesid

Vahepealse suhtega C sadenes ja SiO2 lahustus üleliigses vees

Kõrgel suhtel ei moodustunud kumbki, toimus ainult aktiivne SiC oksüdeerumine

Süsiniku saagise kriitiline faktor on moodustuvate C-sisaldavate gaaside hulk

Nt CH₄ on mittestabiilne kõrgel T, kuid kõrge P suurendab stabiilsust ja seega väheneb C saagis

C. Karbiidide termiline lagundamine:

Kõrgel temperatuuril lagunemine vaakumis või inertgaasi atmosfääris (kõrge T ja alandatud rõhk – metallide välja lendamiseks hea)

Karbiidid sulavad inkongruentselt – karbiidi moodustav element aurustub, sest C sulamistemperatuur ületab enamike metallide oma

Süsinikul on madal aururõhk kõrgetel T-del võrreldes paljude metallidega

Osakeste kuju säilib hästi. Vaakumis lagundamisel võib olla tekkinud süsiniku pinnal näha isegi karbiidil eksisteerinud kriimustusi.

Nanopoorse süsiniku pinna modifitseerimise võimalustest

1. Vedelas faasi oksüdeerimine (näiteks hapetega, nt HNO₃ )

Suurendab eripinda ja poorsust, vähendab tihedust, suurendab pinnal funktsionaalsete rühmade kontsentratsiooni

2. Gaasifaasiline oksüdeerimine (O2, H2O)

Suurendab eripinda ja poorsust, vähendab tihedust, suurendab pinnal funktsionaalsete rühmade kontsentratsiooni

3. Plasmatöötlus (atomaarne hapnik)

Suurendab eripinda ja poorsust, vähendab tihedust, parandab märguvust, suurendab pinnal funktsionaalsete rühmade kontsentratsiooni, vähendab elektrilist takistust, suurendab hapniku redutseerimise elektrokatalüütilist aktiivsust

4. Kuumutamine inertses atmosfääris (N2, Ar jne.)

Vähendab eripinda ja poorsust, suurendab tihedust, enam grafiidilaadsemad struktuurid, vähendab pinnal funktsionaalsete rühmade kontsentratsiooni

10. Elektrokeemilised meetodid (tsükliline voltamperomeetria, konstantse voolu meetod, elektrokeemiline impedantsspektroskoopia) superkondensaatorite karakteriseerimiseks. Kompleksmahtuvus ja kompleksvõimsus. Energia - võimsustiheduse (Ragone) graafikud.

Tsükliline voltammeetria

Elektroodi potentsiaali muudetakse fikseeritud kiirusega, näiteks 1 mV/s või 100 mV/s (potentsiaali laotuskiirus); ühtlase kiirusega muudetakse rakupotentsiaali, selle tulemusena hakkavad ioonid adsorbeeruma pinnale; graafik peab olema võimalikult nelinurkne: nii palju, kui paneme sisse, nii palju saame välja

Mõõdetakse voolu

EKKKde korral peaks olema voltamperogrammi kuju võimalikult lähedane ristkülikuga ning sümmeetriline nullvoolu -joone suhtes -> KEEMILISI REAKTSIOONE EI TOIMU !

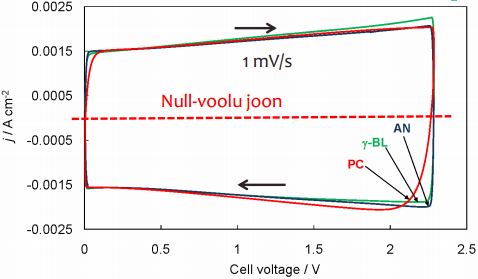tekib ioonide puudujääk, süsteem ei suuda nii kiirelt stabiliseeruda - järelikult pole optimaalseim materjalide valik olnud; sellep tekivad kõrvalekalded ristkülikukujust

Keemiliste reaktsioonide esinemisel leiduvad voltamperogrammidel fikseeritud potentsiaalidel piigid

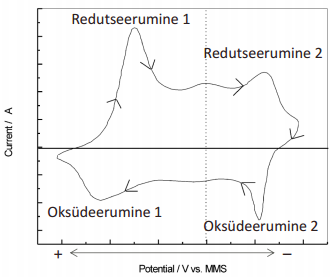
Meetodiga võimalik teada saada:

Optimaalne rakupinge,

Mahtuvuse väärtus,

Hinnanguliselt toimuvate protsesside kiirus (massiülekanne, adsorptsioon),

Keemiliste (kõrval)reaktsioonide esinemine,

Elektrolüüdi lagunemisreaktsioonid,

Orgaaniliste solventide korral vee-lisandi reageerimine,

Redoksmahtuvuslike reaktsioonide korral nende esinemise potentsiaali-vahemik.

„Elektrolüüdi vaesumise“ esinemine.

Impedants-spektroskoopia

Rakendatakse dc vool – elektroodide vahel tekib fikseeritud potentsiaalide erinevus.

Süsteemil lastakse jõuda tasakaaluolekusse.

dc-le lisaks rakendatakse väikse amplituudiga (5 mV) sinusoidaalne ac signaal.

ac mõjul tekkiv signaal väljendatakse kui impedants Z.

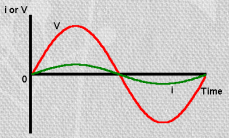Takisti korral: U ja I on samas faasis, kuid I väärtus on peaaegu null

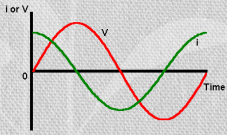
Kondensaatori korral: I on 1/4 tsüklit ees – ehk faasinurk on -90^o (-1/4 täisringist)

f on alati sama U ja I jaoks!

Impedants väljendatakse U ja I signaalide suhtena.

Süsteemi lihtsamaks matemaatiliseks kirjeldamiseks esitatakse impedants komplekssuurusena:

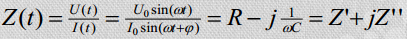
Seega:

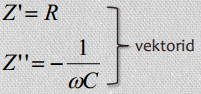
ω = 2πf – ringsagedus

Saadav info spektritest:

Elektrolüüdi ja elektriliste kontaktide takistus Rs (f -> ∞),

Difusiooniline takistus elektroodi materjali poorides,

Mahtuvuse väärtus,

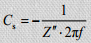
Karakteerne ajakonstant,

aeg, mis kulub ½ kondensaatoris salvestatud energia vabastamiseks.

Rakupinge hindamine, kus algavad lagunemisreaktsioonid.

Energia- ja võimsustiheduste arvutamine:

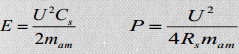
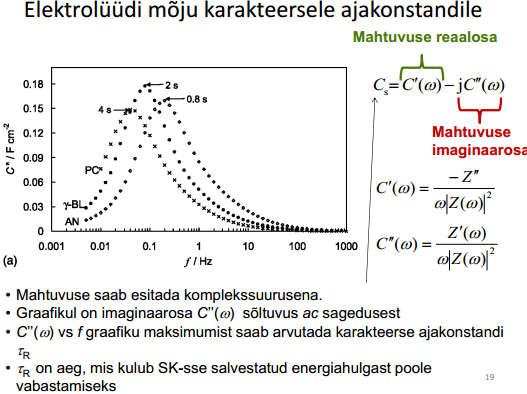
Kompleksmahtuvus ja kompleksvõimsus.

11. Elektrilise kaksikkihi kondensaatorid ehk superkondensaatorid.

Akude elektroodidel toimuvad keemilised reaktsioonid on aeglased, kuid võivad toimuda pikaajaliselt – energia hulk suur, kuid võimsus väike. Ioonide adsorptsioon/desorptsioon EKKK elektroodide pinnal on väga kiire – suur võimsus (salvestatud energia kiire vabastamine), kuid väiksem energia hulk. (Võimsus – energia kasutamise kiirus; Energia – tarvitatud või vabastatud energia hulk sõltub seadme võimsusest ning kasutamise kestusest: Energia = Võimsus x Aeg)

Aku vs SK

Superkondensaator kui sprinter – lühikese aja jooksul annab välja suure koguse salvestatud energiat; Aku kui pikamaajooksja – korraga kättesaadav energiahulk väiksem, kuid pikemaajaliselt.

Seade	Aku	SK
Elektroodi protsess	Elektrokeemiline oks/red reaktsioon	Füüsikaline adsorptsioon
Eluiga (tsükleid)	100... 10 000	<1 000 000
Laadimise/tühjenemise aeg	Mõni minut kuni mõni tund	Mõne sekundi suurusjärgus
Energiatihedus (Wh kg-1)	Kuni 160	0,5 kuni 30
Võimsustihedus (kW kg-1)	1-3	Isegi üle 50
Efektiivsus (%)	50-90	U 95

Energia ja võimsus – sõltub oluliselt elektrolüüdis kasutatavast solvendist: viskoossega väiksem energiahulk kättesaadav. Sõltub töötemperatuurist: madalal temperatuuril massiülekanne aeglane. Seda suurem, mida suurem on mahtuvus, rakupinge. Võimsus sõltub ka rakupingest ja takistusest.

Eluiga – ära määratud selle poolt, kui kondensaator töötab muutliku režiimiga, siis osaliselt võib toimuda elektrolüüdi lagunemise reaktsioon või elektrolüüdi pinnal parasiitsed reaktsioonid. Võib laguneda. Parasiitreaktsioonid tingitud rakupingest jms. Eluiga sadades tuhandetes tsüklites. Võrreldes akudega on eluiga oluliselt pikem, kuna protsess on peaaegu täielikult pöörduv ning ilma keemilise reaktsioonita.

Efektiivsus – elektriline efektiivsus. Peaaegu 100% lähedane. Põhiline languse põhjustaja sisetakistus. Mida suurem võimsusel töötab, seda suurem on takistuse mõju.

SK-s energia salvestamise mehhanism

Elektrilise kaksikkihi kondensaatorid (EKKK)

Elektrostaatiline laengusalvestus

Elektrolüüdi ioonide pöörduv adsorptsioon elektroodil

Elektroodi materjal (enamasti süsinik) suure eripinnaga (m²g^-1) ning väga poorne

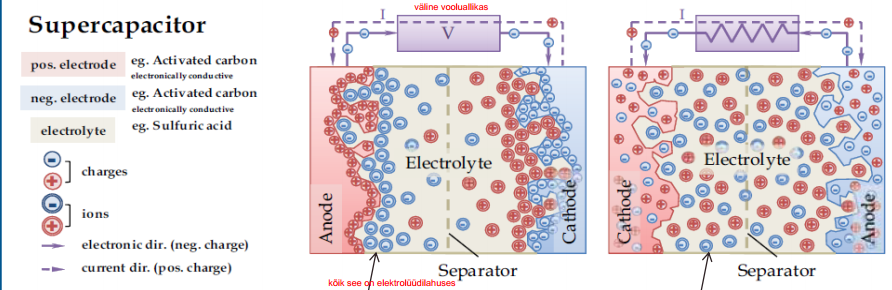
Vasakpoolne on laetud EKKK, parempoolne tühjendatud

Mõlemal elektroodil moodustub EKK, mida võib vaadelda kui tavalist tasapinnalist kondensaatorit, mille mahtuvus avaldub:

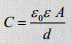
ε₀, ε – vaakumi ja keskkonna dielektrilised läbitavused, d – elektroodide vaheline kaugus, A – elektroodide pindala

Võrreldes traditsioonilise elektrolüütilise kondensaatoriga, on d väga palju väiksem ning elektroodide pindala väga palju suurem ehk mahub rohkem laengut.

EKKKdes on + ja – elektroodid ühesugused, süsteemi võib vaadelda kui kahte järjestikku ühendatud kondensaatorit:

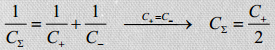
Wikist:

Laengusalvestusest:

elektrienergia salvestatakse elektroodidele (nagu akudeski), kuid mitte keemiliselt

ioonid liidetakse elektroodi pinnale füüsikalise adsorptsiooni teel.

Tänu elektroodi materjali suurele eripinnale >1000 m² /g, ja süsiniku kõrgele erimahtuvusele, saadakse ka märkimisväärsed mahtuvused ~1 F/cm² ühe elektroodi pinnaühiku kohta.

Seetõttu piisab suhteliselt väikesemõõtmelistest elektroodidest, et saada märkimisväärne mahtuvus

SK laadimisel elektrolüüdi positiivselt laetud ioonid, katioonid, liiguvad katoodile (?), tekitades pinnal positiivse laengu

anioonid liiguvad anoodile (+), tekitades sellel negatiivse laengu.

Suurepinnalise süsiniku poorid toimivad seejuures laengusäilitajatena.

oluline optimeerida kogu süsteem selliselt, et kasutatava nanopoorse süsiniku poorid oleksid ioonidele sobivate "mõõtmetega".

Elektroodipaarist moodustub kaks järjestikku ühendatud kondensaatorit C+ ja C?.

Plaatide pindala määrab mahtuvuse

elektroodide vahelisest kaugusest, ehk elektrolüüdiga impregneeritud separaatori paksusest sõltub sisetakistus.

SK-s kogutakse laengud elektroodi pinnalt kokku voolukollektorite kaudu ning kui ühendada välisahelas + ja ? kokku, toimub tühjakslaadimine ja ioonid liiguvad lahuse sügavusse.

Laadimisel protsess kordub taas.

Ehitusest:

koosneb positiivsest ja negatiivsest elektroodist, mille välisküljele on ühendatud voolukogujad (kollektorid) ja sisemisi külgi eraldab separaator.

Kogu süsteem on impregneeritud sobiva elektrolüüdiga ja suletud korpusesse.

Kõrgema pinge saamiseks ühendatakse elemendid järjestikku kondensaatorpatareiks ehk mooduliks.

Pseudomahtuvuslikud kondensaatorid ehk redokssuperkondensaatorid

Pöörduv elektrokeemiline laenguülekande protsess (redoksreaktsioon)

Laeng salvestub läbi pseudomahtuvusliku käitumise – esineb kui termodünaamilistel põhjustel elektroodiprotsessi jätkumiseks vajalik laenguhulk q on rakendatava pinge U pidevalt muutuv funktsioon: C = dq/dU

Toimub mitme-etapiline redoksreaktsioon (mitte üks fikseeritud potentsiaalil toimuv reaktsioon nagu akudes).

Levinumad elektroodi materjalid: d-metallide oksiidid, juhtivad polümeerid, heteroaatomeid (N, O) sisaldavate funktsionaalsete rühmadega modifitseeritud süsinikud

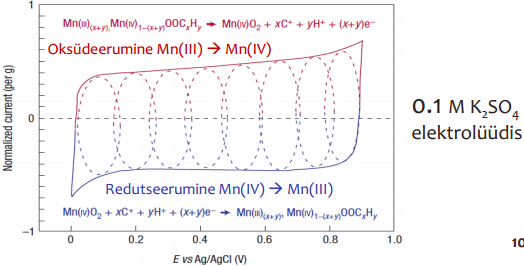
Hübriidsuperkondensaatorid

Asümmeetriline süsteem:

Üks elektrood „aku-tüüpi“ ning teine „SK-tüüpi“

Saavutatav suurem rakupinge

Negatiivne elektrood on „aku-tüüpi“ grafiit, millesse interkaleeritakse Li-ioonid, positiivne elektrood on poorne süsinik, millel toimub anioonide pöörduv adsorptsioon.

Võrreldes EKKKdega, saadakse summaarseks mahtuvuseks kogu „SK-tüüpi“ elektroodi mahtuvus, sest C_aku >> C_SK

Ühtegi kommertsiaalselt kasutatavat veel pole

SK-de ühendamine

SKsid saab omavahel ühendada nii paralleelselt kui ka järjestikku:

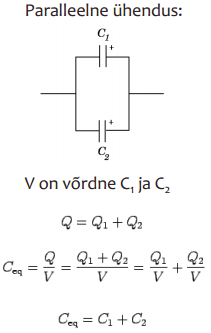
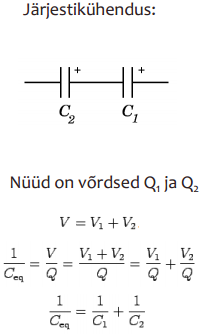
Elektroodimaterjalide, solventide ja soolade valik.

ELEKTROODIMATERJALID

Vajalikud omadused:

Hea juhtivus (vase juhtivust päris omama ei pea, aga ei tohi olla pooljuht või isolaator)

Hea elektrokeemiline stabiilsus

Temperatuuri-stabiilsus

Suur eripindala (1200 ... 1800 m²g^-1)

Avatud poorsus (d_pore= 0.7 ... 4.0 nm)

Võimalikult madal hind

Kergesti töödeldav

Näited:

Süsinikmaterjalid EKKKde jaoks:

Carbon blacks (nn söed)

Aktiveeritud süsiniku pulbrid või kangad

Amorfsed süsinikud (nt karbiidset päritolu süsinikud)

Süsinik nanotorud, sibulad ja nanosarved

Süsinik-aerogeelid

Poorse struktuuri mõju SK karakteristikutele

Elektroodi materjal

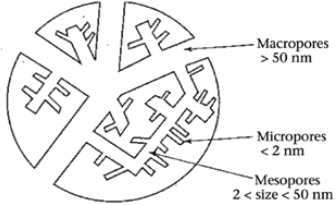Mida suurem on elektroodi materjali eripind (specific surface area - SSA), seda suuremat mahtuvust võib eeldada

Tegelikult on ka kõige poorsemate materjalide mahtuvus limiteeritud

Puudub lineaarne suhe SSA ja mahtuvuse vahel

Osalise või täieliku solvaatkattega ioonid ei mahu väiksematesse pooridesse

Materjal peab olema mingil määral mesopoorne, et tagada ioonide kiire transport mikropooridesse üle kogu elektroodi materjali

Sobivus elektrolüüdiga

Kui poorid solvateeritud ioonidest suuremad, mahtuvus kasvab mõlemal poori seinalt. Kui poorid natuke väiksemad, mahtuvus väheneb, sest ainult 1 kiht ioone mahub, osa ruumi jääb kasutamata. Kui poor väiksem solvateeritud ioonist – mahtuvuse kasv tänu solvaatkatte osalisele eemaldumisele.

I – poorid solvateeritud ioonidest suuremad, mahtuvuse kasv mõlemalt poori seinalt. II – mahtuvus väheneb, sest ainult 1 kiht ioone mahub, osa ruumi jääb kasutamata. III – poori d solvateeritud ioonist väiksem – mahtuvuse kasv tänu solvaatkatte osalisele eemaldumisele.

mida väiksemaks poori muudame, siis ühel hetkel mahtuvus hüppab ülesse > pooridesse lähevad kat/anioonid ilma solvaatkatteta > mahtuvus muutub suureks, aga liikumine on üliaeglaseks muutunud e ajakonstandid muutuvad ülisuureks

vaja leida ideaalne poori laiuse ja iooni suuruse tasakaalu

SOLVENTIDE JA SOOLADE VALIK

Solvent määrab maksimaalse potentsiaalide erinevuse positiivselt ja negatiivselt laetud elektroodide vahel (U).

Kahjuks vee lagunemise termodünaamiline ülepinge (1,23 V) 2–4 korda väiksem kui mõningate orgaaniliste solventide puhul (kuni 5 V).

Vee baasil valmistatud EKKK U ≤ 0,8 V, kuid atsetonitriili (AN) või propüleenkarbonaadi (PC) baasil valmistatud EKKK U = 2,7–3,5 V, sõltudes oluliselt vee (lisandi) kontsentratsioonist EKKKs.

Olulised omadused:

Elektrokeemiline stabiilsus (max U),

0.001% veesisaldus orgaanilises elektrolüüdis vähendab rakendatavat pinget ~10 mV.

Madal viskoossus,

Hea juhtivus,

Suur ioonide kontsentratsioon (hea lahustuvus solvendis),

Kõrge dielektriline läbitavus,

Minimaalne mõju keskkonnale,

Soodne hind.

Vee baasil elektrolüüdid EKKKdes

Elektrokeemiliselt stabiilne kuni ~1 V

Vesilahusega EKKK mahtuvus ~2 korda suurem kui orgaanilistel solventidel põhinev EKKK

Odavam kui orgaanilised solvendid

Võimalik valmistada kõrgema kontsentratsiooniga elektrolüüte

Näiteks:

Vees lahustunud soolad nagu Na₂SO₄ ja NaCl

KOH lahus (1 kuni 6 M)

H₂SO₄ lahus (1 kuni 4 M)

Orgaaniliste solventide baasil elektrolüüdid

Elektrokeemiliselt stabiilne kuni ~3.5 V

Kommertsiaalselt rakendatud tetraalküül-ammonium soolad

Võrreldes H2O baasil elektrolüütidega

Madalam juhtivus (20-50 korda suurem takistus)

Saab kasutada madalamatel temperatuuridel (-50 ^oC)

Atseetonitriil (AN)

Madal viskoossus ja kõrge juhtivus

Kõrge dielektriline läbitavus

Keskkonnakahjulik -> peamine põhjus alternatiivsete solventide/elektrolüütide testimiseks

Propüleenkarbonaat (PC)

Kõrgem viskoossus ja madalam juhtivus vs. AN

Mitte nii kahjulik kui AN

γ-butürolaktoon (γ -BL või GBL)

Viskoossus ja juhtivus võrreldavad AN-ga

Psühhotroopne aine -> ei sobi tarbeesemetes kasutamiseks

Ragone’i kõveratelt on näha, et SK võimsus ja energia sõltuvad oluliselt elektrolüüdis kasutatavast solvendist: Samal võimsusel töötades on näiteks viskoosse propüleenkarbonaadiga kättesaadav palju väiksem energiahulk kui atseetonitriiliga.

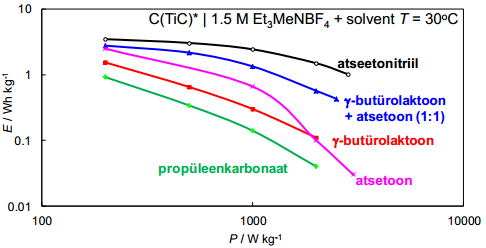
Elektrolüüdi soola mõju: Näha on, et alküülahelate varieerumine oluliselt SK mahtuvuse väärtust ei mõjuta U = 2.5 V korral. (Slaidid SK II)

Ioonsed vedelikud.

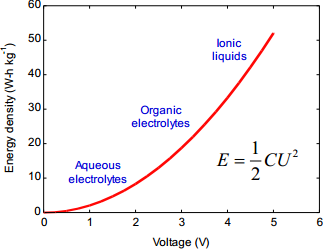
Omadused, eelised-puudused

Ioonne vedelik – toatemperatuuril vedelad soolad

Teoreetiline elektrokeemilise stabiilsuse vahemik ~6 V

Ei saa kasutada madalatel temperatuuridel (kõrge viskoossus)

Võrreldes H2O või orgaaniliste solventidega

+ Väike aururõhk

+ Mitte-süttiv

– Suurem viskoossus

– Madalam juhtivus

– Viskoossuse vähendamiseks ja juhtivuse suurendamiseks:

Võiks kasutada kõrgematel temperatuuridel (kuni 60–80 ^OC)

Lisada väike kogus orgaanilist solventi

Mõju keskkonnale pole selge, kuid üliväike aururõhk vähendab veidi keskkonda sattumist.

Ioonseid vedelikke on palju, kuid kõik pole sobivad EKKK rakenduseks

Näited:

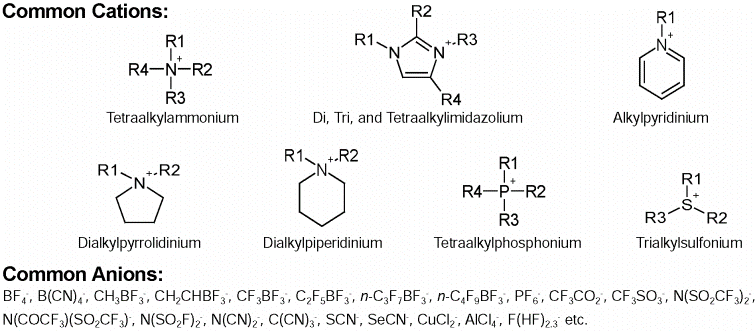
Temperatuuri mõju

Karbiidne süsinik + EMImBF₄

Kõrgematel temp.del moonutusefektid:

EMImBF4 lagunemine,

H₂O ja O₂ jääkide lagunemine,

Funktsionaalrühmade redoksreakts.,

Adsorptsiooni tasakaalu nihkumine desorptsiooni suunas.

Puudub mahtuvuslik käitumine kõrgetel temp.del

Karakteerne ajakonstant τ_R kasvab.

Ehk ei sobi kasutamiseks kõrgel temp.-l!

12. Hübriidkondensaatorid

13. Ühekordsed patareid

Leclanché element:

(–) Zn Zn²⁺ + 2e^–

(+) 2MnO₂ + 2H₂O + 2e^– 2MnOOH + 2OH^– ΔE ⁰ = 1.26 V

C lisatakse MnO₂ juhtivuse parandamiseks

ZnCl₂ elektrolüüt – absorbeerunud (+) poorides ja pasta-separaatoris (nt. tärklis) – “kuiv rakk”

Zn käitub ka kestana ülejäänud elementidele

Eelised:

Odav

Puudused:

Lühike säilitusaeg (kiire iseeneslik tühjenemine)

Suurel voolutihedusel kiire pingelangus

Rakendused:

Taskulambid, suitsuandurid, uksekellad

50 aastat tagasi enamik patareisid

Zn-Mn leelispatarei:

Edasiareng Leclanché elemendist:

Konts. KOH (~30%)

Zn elektrood peene pulbri kujul

Raku ülesehitus vastupidine: MnO₂ segu Zn ja separaatori ümber, elektrilises kontaktis nikeldatud teras-kestaga

Eelised:

Kõrgem efektiivne mahtuvus

Madalam töötemp.

Pikem eluiga >4 aasta 20°C (‘fit and forget’ applications)

Väiksem lekkimisoht vs. Leclanché

Puudused:

Kallim

Rakendused:

Mänguasjad, pardlid, kaamera välk, kellade patareid, jne.

Olemas ka laetavate akudena

Liitium-patareid

(–) Li – e^– Li⁺

(+) Mitmed erinevad (MnO₂, CF_x, MoO₃, V₂O₅ jne.)

Elektrolüüt: LiPF₆ või LiBF₄ lahus orgaanilises solvendis (propüleenkarbonaat, dimetoksüetaan)

Li orgaanilises solvendis stabiilne tänu korrosiooniproduktidest tekkivale kihile

tahke kaitsekiht, mis takistab edasist solvendi pindreaktsiooni

Eelised:

Suur rakupinge ~3.0 V

Kõrge energiatihedus

Aeglane iseeneslik tühjenemine

Lai töötemperatuuri vahemik

Väga kerge

Rakendused:

Back-up mälu, südamestimulaatorite, kellade, kaamerate, kalkulaatorite patareid

14. Laetvad akud ja patareid (panin patareide ja akude põhimõtte + paar näidet akudest)

Energiasalvestusseadmed, milles toimub keemilise sideme energia muundamine elektrienergiaks läbi spontaansete elektrokeemiliste reaktsioonide. Akudes on elektroodideks erinevad elektrokeemiliselt aktiivsed ühendid mitmetes erinevates elektrolüüdi lahustes, mis võtavad tihti ise osa toimuvatest elektroodireaktsioonidest.

Laadimine ja tühjenemine

Aktiivmaterjalidega toimuvaid protsesse esitatakse elektrokeemiliste reaktsioonivõrranditega. Tühjenemisel ühel elektroodil oksüdeerumine, teisel redutseerumine. e ^– liiguvad (–) (+) elektroodile läbi välise vooluahela. NB! Elektrivoolu suund defineeritud (+) (–). Laadimine on protsesside teistpidi suunamine välise vooluallika abil.

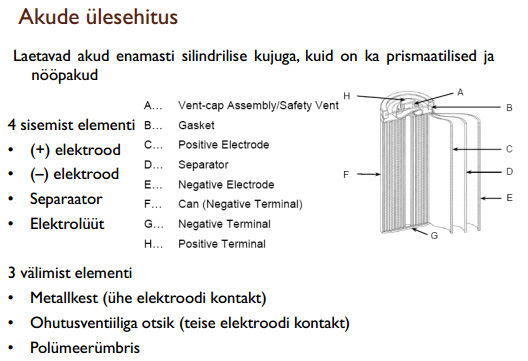
Töövõime hävinemise protsessid:

Aktiivmaterjali tihenemine:

poorsuse vähenemine takistab kättesaadavust elektrokeemiliseks reaktsiooniks

Aktiivmaterjali paisumine ning pudenemine elektroodiplaadilt

Mitteaktiivsete faaside moodustumine:

Tekivad kõrvalreaktsioonil, lagunemisel;

Elektriliselt isoleerivad piirkonnad materjalis

Metalsete nõelte sadenemine:

Lühistumise oht

Voolukollektorite korrosioon:

Suurenenud sisetakistus

Ülelaadimisel gaaside teke elektroodidel:

Läbilöögi efekt

Olulised omadused:

Eluiga

Aku eluea definitsioon – täieulatuslike laadimise/tühjenemise tsüklite arv enne aku mahtuvuse langemist <80% algsest nimiväärtusest

Stabiilne pinge väärtus tühjenemisel

Aku töötamisel on oomiline pingelang (IR)

IR suureneb kõrgetel võimsustel ning sisetakistuse kasvades, kui elektroodireaktsiooni produktid kogunevad ning takistavad edasist reaktsiooni

Kunagi ei lasta akul nö täielikult tühjeneda – tühjenemise pinge alumine piir oleneb vastavast akust

Kõrge energiatihedus (Wh kg^-1) ja võimsus (W kg^-1)

Lai töötemperatuuri vahemik

Aeglane iseeneslik tühjenemine

Iseeneslik tühjenemine – voolutarbija puudumisel elektroodireaktsioonide iseeneslik toimumine

Kiirelt laetav

Ülelaadimise ja ületühjenemise vastupidavus

Usaldusväärne töötamine

Hooldusvaba

Ohutu (ka õnnetuse olukorras)

Valmistatud kättesaadavatest, odavatest ning keskkonnaohututest materjalidest

Tööea lõppedes materjalide taaskasutus/ümbertöötlus

Näiteid:

Pliiakud:

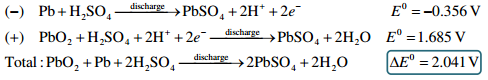
Elektrolüüt, H₂SO₄ võtab osa elektroodireaktsioonidest

Aku laetudolekut saab määrata elektrolüüdi tiheduse järgi.

Tühjenemisel H₂SO₄ H₂O

250-1000 tsüklit, mõjutatud:

Temperatuurist

Töötamine >50 °C vähendab 50%

Tühjenemise ulatus

Keskmiselt tühjenemine ulatuslikumalt – lühem eluiga

Disainitud tühjenema 50–80% ulatuses

Efektiivne laadimise:tühjenemise aegade suhe 5:1

Rakendused:

Sõidukite aku

Tööstus-seadmed (tööriistad)

Stand-by/back-up süsteemid (UPS)

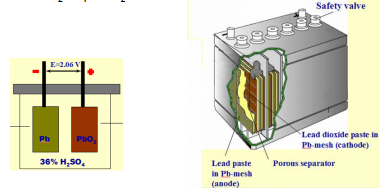
Leelisakudest näide: Ni-Cd

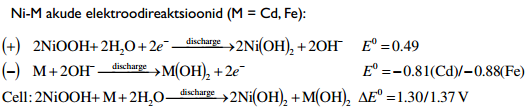
Rakendused:

Elektroonika (kalkulaatorid, kaamerad, lap-topid, taskulambid, jne)

Elektri-/hübriidsõidukid

Militaar- ja kosmoserakendused

Raudtee-tööstus

Stand-by võimsus tööstuses ja elektrienergia tootmises

Eelised:

Koormusele reageerimisaeg mõni ms, annab kohe maksimaalse võimsuse

Efektiivne nii kõrgel kui madalal temp.

Püsiv tühjenemise pinge

Hea tsükleeritavus (<3500 tsüklit)

Ükskõik millises laadimisastmes võib seisma jätta

Kiirem laadimine vs. pliiaku

Puudused:

Kallis

Keskkonnamõju – toksiline lahustuv Cd

Cd raske metall

“Mäluefekt“ – põhjustab akut säilitama väiksemat energiahulka

Kättesaadav energiahulk väheneb, kui korduvalt laadida ainult osaliselt tühjenenud akut

Aku „mäletab" väiksemat mahtuvust

Võib säilitada –20 kuni 40 ˚ C

>32 ˚ C iseeneslik tühjenemine kiirem – eelistatud <21°C

15. Li-ioon-, Li-polümeer, Li-ioon/radikaal akud

Li eelised elektroodi materjalina:

Väga kerge

Kõrge redutseerumispotentsiaal E° = -3.05V

Atraktiivne (–) elektrood

Suurem energiatihedus (Wh kg-1 ) vs. teised metallid

Puudused:

Ei saa kasutada H₂O keskkonnas

Dendriitide moodustumine laadimisel

Võimalikud elektrolüüdid:

LiPF₆ , LiBF₄ , LiClO₄ orgaanilistes solventides (karbonaadid,γ-butürolaktoon, jne.)

Polümeerelektrolüüdid

Ioonsed vedelikud

Keraamilised materjalid

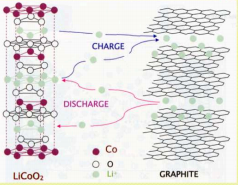Kasutatakse interkaleerumis-elektroode:

Interkalatsiooni all mõeldakse seda, et liitium ioonid saavad siseneda ja väljuda aine kihtide vahelt ilma, et aine kristallstruktuur muutuks.

Grafiiti kasutatakse anoodina seetõttu, et liitiumi interkalatsioon grafiidile võimaldab head reaktsiooni pöörduvust väga madalatel potentsiaalidel.

Aku tühjenemise ja laadumise protsessid on jägmised:

Laadimine: LiCoO₂ + C₆→ Li_1-xCoO₂ + C₆L_x

Tühjenemine: Li_1-xCoO₂ + C₆L_x → LiCoO₂ + C₆

Aku pannakse kokku „tühjenenud“ olekus

Li+ interkaleerumine grafiiti on kiirust limiteeriv protsess

Eelised:

~4.0 V tõttu salvestavad Li-ioon akud rohkem energiat vs. Ni-MH/Ni-Cd (1.2 V)

Samal töörežiimil pikem kestvus laadimiste vahel

Aeglasem iseeneslik tühjenemine vs. Ni-akud

Hooldusvabadus

Püsiv pinge tühjenemisel

Mingi hetk järsem langus, ei tühjendata alla 3 V

Puudused:

Kallis

Ülelaadimine või soojenemine >100 °C lagundab (+)

Vajalik kallite kaitsemehhanismide lisamine

Veega kokkupuutel (–) süttib koheselt

Madalam võimsus vs. Ni-akud, eriti madalal temp.

Li-polümeer

Dõrge dielektrilise konstandiga polümeerid suudavad lahustada Li-soolasid. Polümeer võimaldab pakkida seadme ruumalasse kokku suurepinnalise süsteemi (mitu m²) – suure summaarse voolu. Rullitud silindriks või volditud kokku. Vedeliku puudumise tõttu pole vaja rasket kaitsvat ümbrist

Valmistatakse õhuke polümeerikiht. Kaetakse (–) Li-fooliumiga, komposiit (+) elektroodiga ja voolukollektoritega.

Eelised:

Odavam tootmine vs. Li-ioon

Palju erinevaid võimalusi disainis

Mehaanilisel vigastusel väiksem süttimisoht

Kerge

Vastupidav

Esimeste seadmete piirangud:

Vajalik töötemp. 80–120 ˚C

Küllaltki väike eluiga

Kiirem mahtuvuse vähenemine vs. Li-ioon

Laadimisel samad nõuded, mis Li-ioon aku korral

Hoida kuivas kohas temperatuuril –20 kuni 30 °C

Pikemaajalisel säilitamisel 10 kuni 30 C°

Otsesest päikesevalgusest eemal

Säilitada laadimisastmel 40%

Üle tüki aja laadimisel võib võtta mitu tsüklit nominaalse mahtuvuse saavutamiseks

Rakendused (Li-ioon ja Li-polümeer):

Elektroonika seadmed – praktiliselt kõik mobiilid, laptopid, jne

Elektrisõidukid

Li-ioon/radikaal

Elektroodiks orgaaniline molekulaar-radikaal

Orgaanilisi radikaale saab stabiliseerida keemilise töötlusega tava-T pikaajaliselt eksisteerimiseks:

Radikaali tsentri steerilise stabiliseerimisega

Resonantsstruktuuridega, milles paardumata elektron osaleb

Eelised:

Radikaal-polümeeri elektritakistus väike – väga kiire laadimine (30 s)

Geeli kasutamisel väga paindlik

Rakendused:

Polümeeridel põhinevate Li-akude nišši rakendused üliõhukeste akuplaatidena (näiteks ümber randme keeratavad telefonid jne)

16. Eri tüüpi kütuseelementide võrdlus (töötemperatuur, kasutatav kütus, kasutegur jne)

Töötemperatuurid ja kasutatav kütus erinevatel KE-l:

Madaltemperatuursed (50–150 °C):

Leelis KE (AFC) – puhas vesinik

Polümeer-elektrolüüt-membraan / prootonvahetus-membraan KE (PEMFC) - puhas vesinik

Otsene metanool KE (DMFC) - metanool

Kesktemperatuursed (~200 °C):

Fosforhappe KE (PAFC) - vesinik

Kõrgtemperatuursed (600–1000 °C):

Tahke-oksiid KE (SOFC) – vesinik, CO, metaan, CH₄OH, NH₃, gasoline, H₂S, valik süsivesinikkütuseid

Sulakarbonaat KE (MCFC) – vesinik, CO, CH4, valik süsivesinikkütuseid

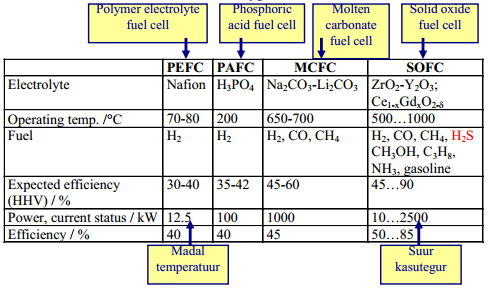
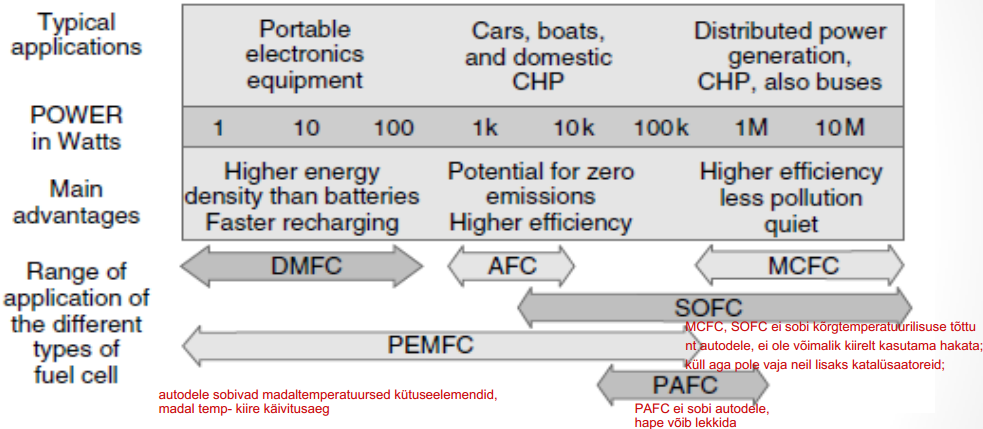
KE tüüp	Tüüpiline elektrolüüt	Rakendused	Eelised	Puudused
Polümeerelektrolüüt- Membraan (PEM)	Perfluorosulfoon- Hape	Väikese võimsusega elektri tootmine, Kaasaskantav energia, tagavara energiaallikas, Hajutatud tootmine, Transport, eritranspordivahendid	Tahke elektrolüüt vähendab korrosiooni ja probleeme käsitlemiselm, madal T, quick start-up	Kallis katalüsaator, Tundlik kütuse ebapuhtuste suhtes, low temp waste heat
Aluseline (AFC)	KOH vesilahus soaked in matrix	Sõjaväetehnikas Kosmoses	Katoodne reaktsioon aluselises kk-s kiirem > suur jõudlus, Odavamad komponendid	Kütuses ja õhus leiduva CO2 suhtes tundlik, elektrolüüdi käsitlemine
Fosforhape (PAFC)	Fosforhape soaked in matrix	Hajutatud tootmine, Elektri ja soojuse koostootmine	Kõrgem T võimaldab CHP’d, suurem tolerants kütuse ebapuhtuse osas	Pt katalüsaator, Pikk stardiaeg?, Madal vool ja võimsu,
Sulakarbonaat (MCFC)	Li/Na/K-karbonaadid soaked in matrix	Electric utility, Hajutatud tootmine, Elektri ja soojuse koostootmine	Kõrge efektiivsus, Fuel flexibility, Katalüsaatoreid võib varieerida, Sobib CHP’le	Kõrgetemperatuuriline korrosioon ja raku komponentide lagunemine, pikk stardiaeg, madal energiatihedus
TOKE	Ütriumoksiidiga stabiliseeritud strontsiumoksiid (Y2O3-ZrO2)	Electric utility, Hajutatud tootmine, Auxiliary power Elektri ja soojus koostootmine	Kõrge efektiivsus, Fuel flexibility, Katalüsaatoreid võib varieerida, Tahke elektrolüüt, Sobib CHPle ja CHHPle, hübriid/GT tsükkel	Kõrgetemperatuuriline korrosioon ja raku komponentide lagunemine, kõrge temperatuur vajab pikka stardiaega

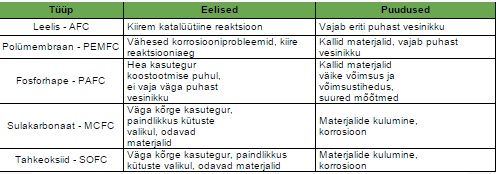
KEde rakendused

Statsionaarsed elektrijaamad (koostootmisjaamad)

Väiksemamahulised (300 kW kuni 2 MW) individuaalseks kasutuseks

Suurema mahuga (1-10 MW) hajutatud elektrienergia tootmise süsteemis

Eelkõige sõltumatu energiavaru olemasoluks nt haiglates, tööstuses, ettevõtetes, jne

Kütuseks maagaas või süsi (gaasistatud) või vesinik

Hinna optimeerimisel ning laiadasel kommertsialiseerimisel võiks KEsid rakendada ka baasvõimsuse tootmiseks nende suure efektiivsuse tõttu

Elektrisõidukite liikumapanev jõud (kütus)

Null-emissiooniga sõidukid H₂ kütuse korral

Pardapealne elektrienergia kosmosesõidukitele, allveelaevadele jt suletud süsteemidele

Juba 1960ndatel demonstreeriti PEMFC ja AFC kasutamist kosmoseprogrammis

Portatiivsete elektrooniliste seadmete energiaallikas

17. Madaltemperatuursed kütuseelemendid

Madaltemperatuursed (50–150 °C):

Leelis KE (AFC) – puhas vesinik

Polümeer-elektrolüüt-membraan / prootonvahetus-membraan KE (PEMFC) - puhas vesinik

Otsene metanool KE (DMFC) – metanool

Leelis KE (AFC)

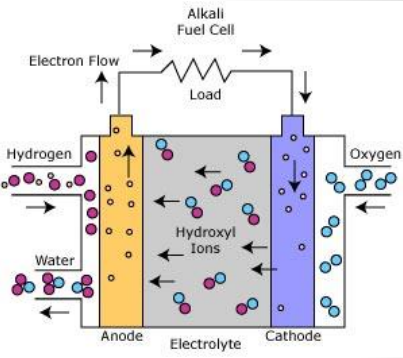
Elektrolüüt: Konts. KOH (85 %) töötemp. ~250 °C

Elektrolüüt paikneb tahkes maatriksis (asbest)

KOH – kõrgeima juhtivusega leelistest

Anoodil olevad katalüsaatorid: Ni, teras, Pt-Pd

Katoodil olevad katalüsaatorid: NiO, Ag, Au-Pt

Kütus: puhas H₂

CO endiselt katalüsaatori mürk

CO₂ reageerib KOH-ga, moodustades K₂CO₃

Vähenenud OH konts. – mõjutab kineetikat

Elektrolüüdi viskoossus kasvab (difusioon ja juhtivus)

Sadenemine poorses elektroodis – vähenenud massitransport

Väheneb O₂ lahustuvus

Eelised/puudused:

Eelised:

Kiirem O₂ redutseerumine aluselises keskkonnas

Kõrgema töötemp tõttu laiem katalüsaatorite valik (Ni, Ag, metalloksiidid ja väärismetallid)

Puudused:

CO₂ tundlikkuse tõttu vajalik ülipuhas H₂

Väga efektiivse CO ja CO₂ eemaldamise süsteemiga reformer või elektrolüüsitud H₂

Õhu kasutamisel oksüdeerijana, tuleb ka sealt CO₂ eemaldada

Tehniliselt lihtne – aga süsteemi suurus/hind

Edukalt kasutatud kosmoserakendustes

Polümeer-elektrolüüt-membraan / prootonvahetus-membraan KE (PEMFC)

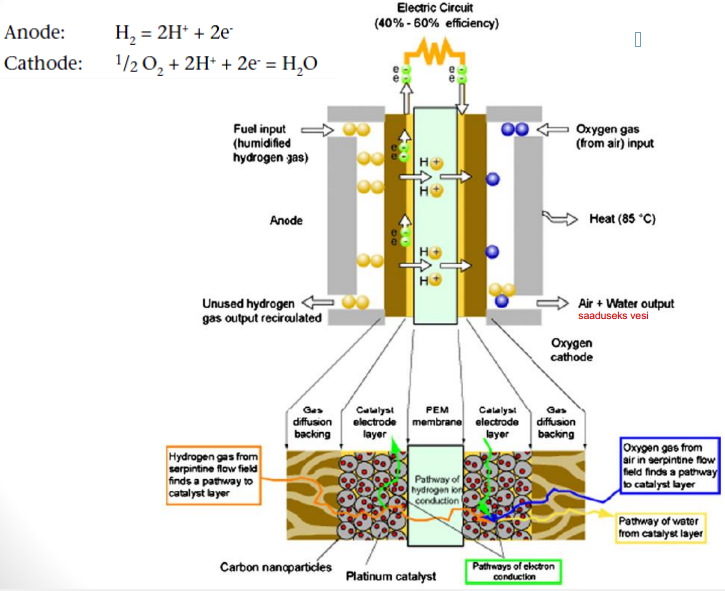
Loengus: Prootonite liikumine anoodilt katoodile; kui kasutatakse katalüsaatoreid, siis reaktsioon toimub katalüsaatori säästmiseks poorse struktuuri lähikihis; ka katoodil käib reaktsioon aktiivkihis, mis võimalikult elektrolüüdi lähedal; elektrolüüdi materjaliks on poorne membraan.

PEMFC koostisosad

Polümeer-membraan prootonjuhina (ionomeer)

Polymer electrolyte membrane / proton exchange membrane

Fluoreeritud sulfoonhappe polümeer või muu sarnane polümeer (Nafion®)

–SO₃H rühmad võimaldavad H⁺ liikumist läbi materjali

Max juhtivuseks peab polümeer olema niisutatud (aga ei tohi olla ka liiga niiske), samas elektroodi pinna läheduses peab olema piisavalt kuiv gaaside takistuseta transpordiks

Minimaalne gaaside läbilaskvus

Loengus: H ei tohi sattud katoodiruumi, O ei tohi sattuda anoodiruumi > muidu kogu süsteemi efektiivsus väheneb

Anood ja katood – suure eripinnaga (et oleks võimalikult palju reaktsioonitsentreid) süsinik-materjal katalüsaatori (Pt – sellepärast kallis) nanoklastritega

Ionomeeri lisand sideainena ja H+juhtivuseks

Süsinikkandja – “ gaasi difusiooni kiht ”

Voolukollektor/vahelüli

Grafiidist või metallist

Gaasivoolu kanalitega

Reaktantide jäägi ja vee ärajuhtimine

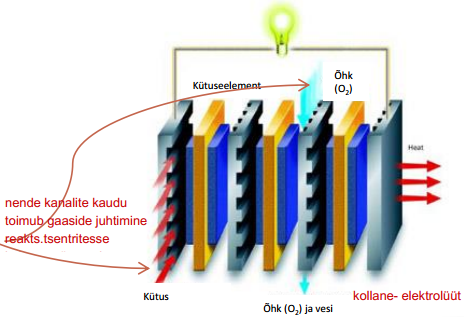
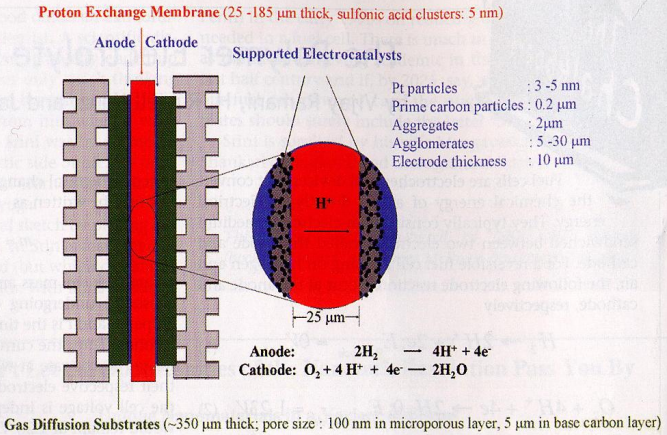
Loengus: Mida paksem membraan, seda suurem sisetakistus > soovitatakse võimalikult õhukest membraani

Eelised/puudused

Eelised:

Madal töötemp. – kiire käivitamine (start-up)

Tahke membraan-elektrolüüt – hea takistus gaasi ülekandele

Korrosiooni probleem väike (vesi ainuke vedelik)

Suur võimsus (mitme ühikraku kokkupanek võimalik > võimalik võimsust varieerida)

Lihtne skaleerida (ühikrakkude ühendamine, elektroodide mõõtmete muutmine)

Puudused:

Madal ja kitsas töötemp. vahemik – keeruline termiline regulatsioon (eriti kõrgel voolutihedusel) ja jääksoojuse kasutamine

Vee regulatsioon – membraani niisutamine vs. Üleujutamine

Aktiivse katalüsaatori (Pt) vajadus vs. kõrg-temp KE

Aeglane O2 redutseerumise reaktsioon

Kallis membraan

Väga tundlik kütuse lisandite suhtes (CO, S jne)

PEMFC kommertsialiseerimise takistused

Vastupidavus

Keemiline rünnak membraanile – katoodireaktsiooni kõrvalprodukt H₂O₂ põhjustab õhenemist, gaasi lekkimist läbi membraani, lühistumist

Katalüsaatori mahapudenemine elektroodilt

Katalüsaatori tundlikkus (CO <10 ppm)

Adsorbeerunud CO eemaldamine – kiirust limiteeriv

Lihtsustatud CO oksüdeerimine adsorbeerunud OH abil (Ru katalüsaatoril madal potentsiaal OH-ads moodustumiseks)

Hind

Katalüsaatori osakeste suuruse vähendamine ja homogeensem jaotamine

Uued katalüsaatorid – nt Pt-sulamid, mitte-väärismetallid

Uued sulfoneeritud süsivesinikud ja happega dopeeritud polümeerid

Soojenemine ebaefektiivsuste tõttu – peamiselt aeglane O₂ redutseerumine

PEMFC membraan

Membraani omadused optimeerimiseks:

Prootonjuhtivus – sõltub sulfoneerimise ulatusest ja membraani paksusest

Mehaaniline, keemiline ja termiline vastupidavus (sobiva süsinik-peaahela valimine)

Tugevdavad lisandid

Gaasi läbilaskvus – sõltub materjalist endast ning membraani paksusest

Sisetakistus minimaalne õhukese kihi korral

NafionTM

Kallis (~780 $/m²)

Kõrge O2 läbilaskvus

Limiteeritud töötemp (T < 80 ^oC)

CH₃OH, CH₄ läbilaskvus (sõltub T)

Polüstüreen ja divinüülbenseen sulfoon-gruppidega

H₃PO₄-ga modifitseeritud polümeerid

H-soolasid (CsHSO₄, NaH2PO₄) sisaldavad polümeerid

Rakendused:

Back-up energia

Kaasaskantav energia

Elektri hajutatud genereerimisel

Sõidukites

Otsene-metanool KE (DMFC)

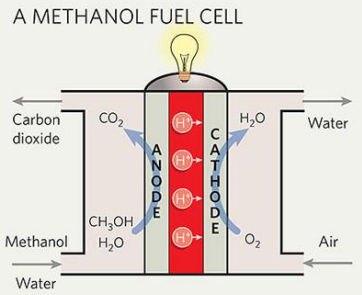
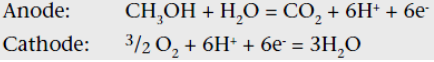
Loengus: samamoodi toimub prootonite juhtimine, aga anoodi suunas toimub metanooli liikumine

Modifitseeritud PEMFC, mis kasutab kütusena metanooli

Vedel kütus vs gaasiline – MeOH oluliselt lihtsam transport ja hoiustamine

Väike MeOH molekul käitub H₂O-le sarnaselt – tungib läbi kasutatavate membraani materjalide

Kütuse kadu

Madal rakupinge (0.25-0.4 V):

Pingekadu segapotentsiaali tõttu O₂-elektroodil (toimub ka kütuse redutseerimine)

MeOH laguproduktide (nt CO) adsorptsioon elektroodidel

CO-taluva katalüsaatori vajadus veel suurem vs PEMFC (katalüsaator ei tohi Coga reageerida)

Pt katalüsaatorit vaja 10x rohkem (3-5 mg/cm²) vs PEMFC

Sihtmärk parema T-taluvusega membraan:

Kõrgemal töötemp. CO tundlikkus väheneb

>100 °C – H+ juhtivuse parandamises ei saa vesi osaledaM

MeOH ülekande vähendamiseks vajalik madala elektro-osmootse ülekandekoefitsiendiga materjal

Materjalid on üldiselt samad, mis PEMFC-l:

Elektroodid: katalüütiline kiht koosneb süsiniku nanoosakestest, katalüsaatorist (Pt) ionomeerist, et oleks nii elektron- kui ka ioonjuhtivus; gaasi difusioonikiht koosneb süsinikust ja teflonist üldiselt, peab olema hüdrofoobne materjali O₂ ja CO₂ ärastamiseks elektroodidelt (vastavalt katoodilt ja anoodilt)

Membraan: nt perfluorosulfoonhappe polümeer.

Eelised: Pole vaja kütuse reformimist, hea energia ja võimsustihedus

Puudused: MeOH toksilisus, Madal efektiivsus

Rakendused mikrokütuseelementidena elektroonilistes seadmetes (nt mobiiltelefonid)

18. Tahketel oksiididel põhinevad ioonjuhid ja tahkeoksiidsed kütuseelemendid

Tahketel oksiididel põhinevad ioonjuhid

Tahkeoksiidsed kütuseelemendid

Kuna siin on materjalide poolest tegu keraamikaga, siis purunemisohu tõttu sõidukitele ei sobi.

KE liik, milles kõik funktsionaalsed elemendid on tahkes faasis

Elektroodid on poorsed kompleksoksiidid ning elektrolüüt tihe oksiidne kiht

KE summaarne elektroodide protsess eksotermiline – soojust ära juhtida

Suure koormusega ülekuumenemine

Sisetakistuse ja voolu mõjul

Kütuse reformimine endotermiline – KEst saadava soojuse abil

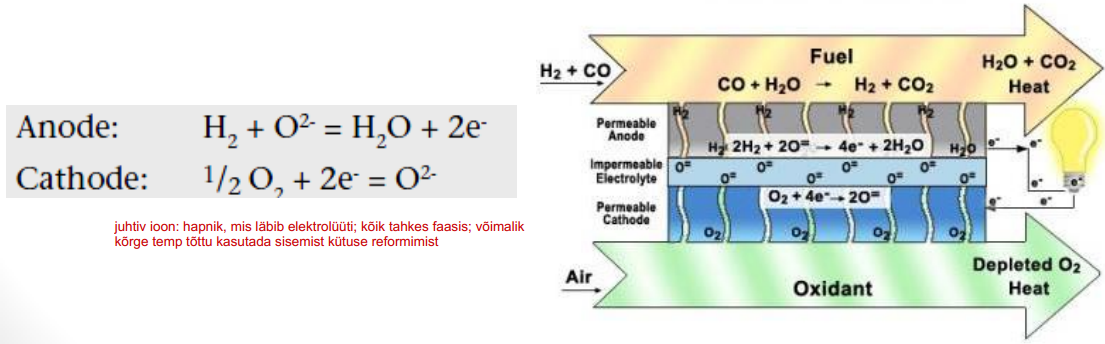
SOFC elektrolüüt

Tahke mittepoorne metalloksiid

O^2-(või H⁺) juhtiv kompleksoksiid (hapnikjuhtivaid väga vähe)

Tihe materjal (gaaside ülekandeta)

Võimalikult õhuke (sisetakistus)

Õhuke (~40 μm) tihe kiht sünteesitakse otse poorsele elektroodile

Parim meetod elektrokeemiline aursadestus (EVD) – saadakse puhas ning väga tihe kiht (kasutatakse ka sukeldamist, pihustamist ja lamineerimist-paagutamist (kilega)

Alternatiivideks:

Pihustuskatmine

Sukelduskatmine

Lamineerimine järgneva paagutamisega

Nanoosakeste (5-10 nm) suspensiooniga kaetakse õhukeste (20 μm) kihtidena

Osakeste suuruste jaotus ja dispergeerumine pastas olulised faktorid

Levinuim ütrium-stabiliseeritud tsirkooniumoksiid (YSZ)

Y₂O₃ lisand stabiliseerib ZrO₂ kuubilise struktuuri kõrgel töötemperatuuril ning tekitab O-vakantse

Tüüpiliselt 10 mol% Y₂O₃

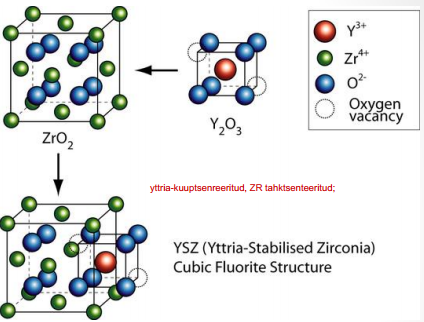
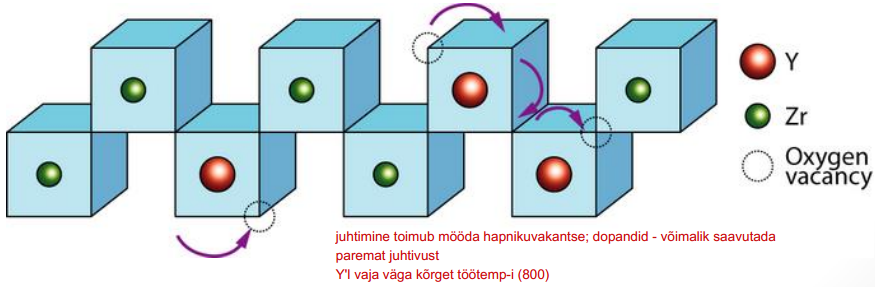
CeO2 samuti uuritud elektrolüüt (dopeeritud nt Gd-ga) (kõrgematel T-del suuremad juhtivused)

Eelised:

Kõrge ioonjuhtivus

Efektiivne madalamal T (<700 °C)

Laiem valik (odavamaid) materjale teiste komponentide jaoks

Puudused:

Kipub redutseeruma kütuse poolel

Madalamal töötemp. (500-700 °C) suur osakeste piirpinna takistus ioonjuhtivusele

SOFC elektroodid

Anood: Ni/kompleksoksiid (uuritud ka Co, Fe, grafiit)

Hea elektrijuhtivuse tõttu on metallid atraktiivsed anoodi materjalid

Ni kasutamise probleemid:

Soojuspaisumine liiga kõrge, et kombineerida elektrolüüdiga

-> Ni-YSZ komposiitanood (või muu oksiidiga)

Kipub töötemp.-l agregeeruma ja sulgema poorsust

Katalüüsib grafiidi moodustumist süsivesinikest

Sadenenud grafiit vähendab elektroodi efektiivsust

Kaob SOFCi põhiline eelis – lai kütuste valik

Katood: LaMnO3 või LaCoO3 (perovskiit tüüpi*) dopeeritud haruldase muldmetalliga (nt Sr, Ce, Pr) juhtivuse parandamiseks

Keemiline vastupidavus oksüdeerivas keskkonnas

Eelised/puudused

Eelised:

Tahke elektrolüüdiga täpsem kolme faasi piirpinna kontroll

Elektrolüüt ei ujuta elektroode

Kiire kineetika

Pole ülikalleid katalüsaatoreid

CO on kütus

Puudused:

Paisumiskoefitsientide ühildamine

Piiratud materjalide valik kõrgel T töötamiseks

Raske saada kõiki kihte õhukesi – takistus!

Detailide valmistamise keerukus

65