Dokumendid > Keemia > Füüsikaline > Kollokviumi vastuses aines Füüsikaline keemia

Füüsikaline keemia I; 2012 aasta sügissemester

Esimene kontrolltöö (aka kollokvium)

Kollokviumiküsimused

Küsimustega tutvumisel tuleb arvestada, et

kui küsimuses on märgitud (tuletuskäiguga) siis peab tuletuskäiku oskama. Küsimus võib kollokviumi tulla aga ka ilma tuletuskäiguta).

Kollokviumis võivad olla erinevad küsimused ka ühte küsimusse kokku pandud.

GAASID

Ideaalse gaasi seadused.Standardolekud gaaside korral

Boyle seadus: kindla koguse ja temperatuuriga gaasi korral on ruumala ja rõhu korrutis konstantne

Charles`i seadus: Konstantsel rõhul on ruumala võrdeline temperatuuriga

Gay-Lussac'i seadus : gaasi rõhk on võrdeline temperatuuriga, kui gaasi ruumala ja hulk ei muutu

Avogadro printsiip : Kui temperatuur ja rõhk ei muutu, siis on gaasi ruumala konstantne

NORMAALTINGIMUSED: t=0ºC ja rõhk 1 atm

STANDARDTINGIMUSED: t=25ºC ja rõhk 1 bar

Ideaalse ja reaalse gaasi võrdlus. Ideaalse gaasi olekuvõrrand ja reaalse gaasi olekuvõrrand (va der Waalsi võrrand)

Ideaalgaasil puuduvad osakestevahelised vastastikmõjud, reaalsetes gaasides asuvad osakesed üksteisele piisavalt lähedal (kui rõhk suurem, temp madal) et nende vahele tekivad van der Waalsi jõud. Ideaalgaasi siseenergia sõltub ainult temperatuurist; reaalgaasi siseenergia sõltub ka tema ruumalast- teisisõnu, reaalgaasil on siserõhk. Lisaks on reaalgaasi osakestel omaruumala, ideaalgaasil omaruumala puudub. Erinevalt ideaalgaasist muutub reaalgaas teatud rõhul ja temperatuuril vedelaks.

pV=nRT vs

Ideaalsete ja reaalsete gaaside võrdlus seoses osakestevaheliste toimetega

Ideaalgaasis toimuvad osakeste vahel ainult elastsed põrked. Reaalgaasis mõjuvad osakeste vahel suured tõukejõud kui osakesed väga-väga lähedal ning tõmbejõud kui os vaheline kaugus on suurusjärgus mõni osakese diameeter. (Võib-olla saaks siin rääkida ka kokkusurutavustegurist? Et reaalgaase on tõmbejõudude tõttu mõistlikutel rõhkudel lihtsam kokku suruda kui ideaalgaase; suurte rõhkude korral aga väga palju raskem kokku suruda.)

Molekulidevahelised toimed

Kaugtoimed: ioon-ioon; ioon-dipool; ioon-induts dipool; dipool-dipool; dipool-indutseeritud dipool; dispersioonijõud

Lähitoimed: Tõukejõud

Ideaalsete gaaside segud, osarõhkude ja moolmurdude seosed (Daltoni seadus). Ideaalse gaasi

olekuvõrrand gaaside segu korral.

(Partsiaalrõhk ehk osarõhk p _j on jõud, mida avaldavad gaasi j molekulid anuma ühikulise suurusega seinale.)

Daltoni seadus : Rõhk, mida avaldab gaaside segu, on võrdne üksikute gaaside osarõhkude summaga.

Kehtib ideaalgaaside puhul, st mol vahelised interaktsioonid puuduvad

p _j X _j p võrdeteguriks

Asendades üldrõhu pV=nRT järgi, siis see võrrand kehtib ainult ideaalgaaside puhul

p _j=X _j p =

Ideaalse gaasi siseenergia, entalpia ja soojusmahtuvuse molekulaarkineetiline tagapõhi

SISEENERGIA: Gaasimolekuli energia võib jaotada 2 ossa: temp sõltumatu (U ₀ ) ja sõltuv osa (U t ) temp sõltuv osa on seotud molekuli kin energia kasvuga temp tõstmisel. Selle ja liikumise vabadustusastmete arvu a vahel on seos:

U = N_Aε = N_Aε₀ + N_Aε_t = U₀ + U_t U_t ja liikumise vabadusastmete vaheline seos:

ENTALPIA: Kuna H= U+pV ja ideaalgaasi korral pV=RT, siis saame avaldise molaarse entalpia jaoks:

SOOJUSMAHTUVUS: Kuna

Analoogselt saame entalpia kaudu soojusmahtuvuse sõltuvuse rot vabadusastmete arvust konstantsel rõhul:

Ideaalgaasi molekulide ruutkeskmise kiiruse temperatuurist sõltuvuse võrrand ja üheaatomilise gaasi keskmise kineetilise energia temperatuurist sõltuvuse võrrand (tuletuskäiguga, arvestades gaaside molekulaarkineetilises teoorias tuletatud võrrandit

Üheaatomilise gaasi osakeste keskmine kineetiline energia on

Gaasiosakeste kiiruste Maxwelli jaotuse

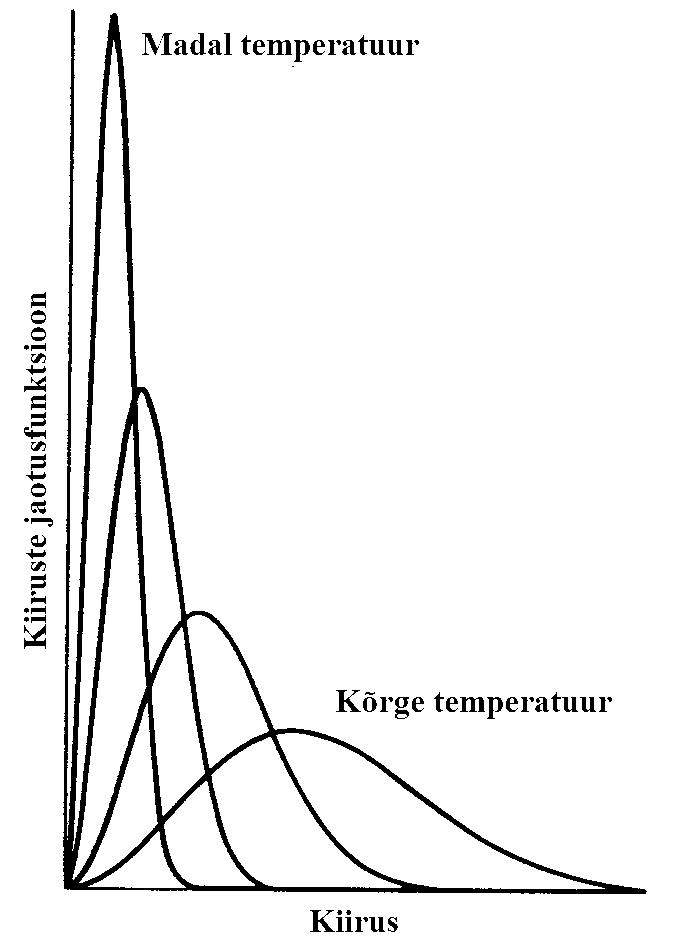
Maxwelli jaotus esitatakse tavaliselt dN/(Ndv) sõltuvusena kiirusest v. Joonisel on toodud kiiruste jaotusfunktsioon sõltuvalt temperatuurist. Kõvera maksimumile vastab osakeste kõige tõenäolisem kiirus. Mida kõrgem on temperatuur seda suurem on osakeste kõige tõenäolisem kiirus. Kõige tõenäolisem kiirus ei pruugi kokku langeda aritmeetilise keskmise kiiruse ega ka ruutkeskmise kiirusega.

Kõrgemate temperatuuride korral on osakeste kiirused rohkem hajutatud; madalamatel vähem hajutatud. See tähendab, et madalamatel temperatuuridel liigub kõige tõenäolisema kiirusega valdav enamus osakesi, kõrgematel temperatuuridel on nö hälbijaid rohkem.

Gaasimolekulide ruutkeskmise kiiruse sõltuvus temperatuurist ja molaarmassist ning nähtused, mis molekulaarkineetilise teooria paikapidavust kinnitavad.

kui temperatuur ei muutu, siis gaasi efusiooni kiirus on pöördvõrdelises sõltuvuses gaasi molaarmassi ruutjuurega

Aritmeetiline kiirus, ruutkeskmine kiirus ja kõige tõenäolisem kiirus.

Ruutkeskmine kiirus
Aritm keskmine kiirus
Kõige tõenäosem kiirus

Kuidas sõltub puhta gaasi osakeste põrkesagedus ning osakeste vaba tee pikkus osakeste suurusest, rõhust ja temperatuurist?

Vedelikusamba rõhk (hüdrostaatiline rõhk) ja gaasisamba rõhk (baromeetrilise jaotuse seadus) (tuletuskäiguga)

Olgu meil vedelikusammas kõrgusega h ja ristlõikepindalaga A. Alusele mõjub jõud F=mg=pA kuna m=?V ja V=Ah , saame et anuma põhjale mõjuv rõhk on p=?gh

Liikudes nivoolt 1 nivoole 2 samba kõrgus kasvab, aga rõhk väheneb, seega dh-le vastab -dp; dp=-?gdh ; üldjuhul sõltub tihedus rõhust, vedelikud aga on halvasti kokkusurutavad ning nende korral saab valemi lihtsalt integreerida: (kui h₁ =0, siis) p – p ₀ = -?gh ₀

Gaaside tihedus sõltub rõhust. Ideaalgaaside korral on see sõltuvus:

asendame võrrandis tiheduse ja eraldame muutujad:

Siit valemist on näha, et rõhu suhteline muutus ei sõltu, milliselt kõrguselt gaasismmast vaadelda. Eelneva võrrandi integreerimisel saame baromeetrilise jaotuse seaduse:

Van der Waalsi toimed. Osakestevahelise toime potentsiaalse energia sõltuvus osakestevahelisest kaugusest.

4 küs +Kui molekulid ei puutu vahetult kokku (kui osakestevaheline kaugus on suurem kui u 2 molekuli diameetrit d), siis domineerivad tõmbejõud. Osakestevahelised tõukejõud on olulised, kui osakesed on üksteisele väga lähedal. Tõukejõude nimetatakse lühitoimejõududeks ja need domineerivad, kui kaugus r kahe molekuli vahel on võrreldav molekuli diameetriga. Osakestevaheliste tõukejõudude tõttu langeb kõrgetel rõhkudel oluliselt reaalgaaside kokkusurutavus. Kokkusurutavuse piiri määrab osakeste omaruumala. Ideaalgaasil omaruumala puudub.

Gaaside kondensatsioon ja kriitilised parameetrid (selgitada rõhu ruuma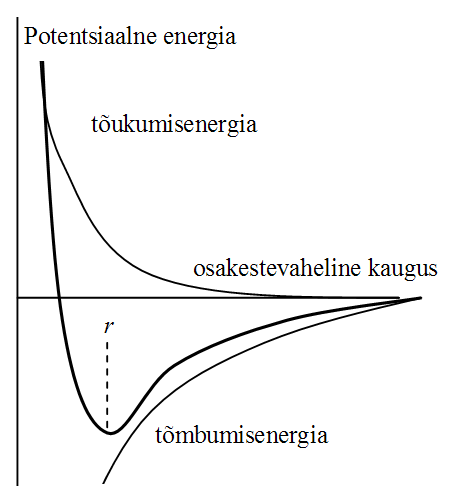last sõltuvuse graafiku alusel)

Surume reaalgaasi kokku isotermiliselt temperatuuril t1. Punktist A punktini B allub gaas ideaalse gaasi seadusele (pV=const). Punktis C minetab gaas ideaalgaasi omadused ja kuni E-ni saab gaasi kokku suruda, ilma et rõhk (aururõhk sel temp-l) muutuks. C kuni E-ni on silindris vedela ja gaasilise oleku tasakaal ja neid faase eraldab piirpind.

Vaadeldes isotermi, mis vastab kriitilisele temp-le selgub, et pole enam kondenseerumisele vastavat platood- sellest temp kõrgemal pole enam võimalik gaasi veeldada. T _c isotermil asuvat käänupunkti nim kriitiliseks punktiks, sellele vastavat rõhku kriitiliseks rõhuks ja ruumala kriitiliseks ruumalaks. T _c -st kõrgemal ei teki enam teravat eralduspinda gaasi ja vedela faasi vahel.

Reaalse ja ideaalse gaasi kokkusurutavustegur. Kokkusurutavusteguri seos gaasi viriaalisotermiga.

Gaaside kokkusurutavustegur näitab, kui palju erineb reaalne gaas ideaalsest ning iseloomustab reaalgaasi kokkusurutavust. Ideaalgaasi kokkusurutavustegur Z=1; Reaalgaasi kokkusurutavustegur Z:

*kui rõhk p on madal, siis Z umbes 1;

*kui p >> 1, siis Z > 1, s.t. reaalseid gaase on raskem kokku suruda kui ideaalseid;

*vahepealsetel rõhkudel enamiku gaaside korral Z < 1, sest valitsevad tõmbejõud, mis aitavad gaasimolekule koos hoida.

SEOS VIRIAALISOTERMIGA: reaalgaas dZ/dp= B' + 2*C'p+... =umbes B' kui

p ? 0 ehk teisiti öelduna väikese rõhu muutuse korral muutub kokkusurutavustegur B' võrra. Ideaalgaasi puhul dZ/dp=0

Taandatud parameetrid ja vastavate olekute printsiip.

Gaaside iseloomustamise suhtelisel skaalal on rõhk, ruumala ja temperatuur on jagatud temale vastava kriitilise parameetriga. Neid jagatisi nimetatakse taandatud parameetriteks.

VASTAVATE OLEKUTE PRINTSIIP: Erinevate gaaside T _r ja p_r on võrdsed kui V _r on sama. Ehk samal taandatud temperatuuril on gaaside kokkusurutavustegur ligikaudu sama ja kõrvalekalded ideaalsusest võrreldavad.

Reaalgaaside kirjeldamiseks ei ole leitud ühte universaalset olekuvõrrandit. On koostatud terve rida teatud piirides kehtivaid olekuvõrrandeid. DdW taandatud parameetritega olekuvõrrand on universaalne; kahjuks aga ainult kerakujuliste molekulide korral

Selgita van der Waalsi isotermi parandusliikmete olemust. Võrdle reaalgaasi viriaalisotermi ja van der Waalsi isotermi. Milline on nende isotermide seos ideaalgaasi olekuvõrrandiga?

Liige “n*b” võtab arvesse, et vaba ruumala, milles molekulid liikuda saavad on väiksem kui ideaalgaasi korral. Arvestab molekulide omaruumala.

Rõhu parandusliige

võtab arvesse osakestevahelisi vastastikmõjusid proportsionaalsed gaasi molaarse kontsentratsiooniga.

Viriaalisotermi võrrand on kasutatav 1 konstantse temperatuuri piires; vdW võrrand kehtib erinevatel temperatuuridel ja on üldisem. Viriaalisoterm on eelistatud, kui tahetakse täpsemaid ja usaldusväärsemaid tulemusi. VdW võrrandi eelis on aga see, et ta on analüütiline (sümbolitega väljendatud) ja annab võimaluse teha üldistavaid järeldusi reaalgaaside kohta.

Selgita ideaalgaasi ja reaalgaasi isotermide (p,V-sõltuvuste) erinevusi.

Reaalgaas võib kondenseeruda ja seega tekib platoo isotermi graafikule (temperatuuril alla kriitilise). Ideaalgaasi isotermil platood ei teki; samuti pole ideaalgaasil kriitilisi parameetreid.

VdW isotermid; jättes välja vahepeal kahanemise (Atkins lk 20), kirjeldavad reaalgaase üpris hästi. Isotermi võnkumine aga on ebarealistlik, sest see vihjab, et mingitel tingimustel ruumala vähenemisel rõhk kahaneb. Seega asendatakse võnkepiirkond horisontaalse joonega nii, et mõlemale poole jääks võrdne graafiku pindala. See joon tähistab piirkonda, kui gaas kondenseerub.

Kriitilisest temperatuurist kõrgemal meenutavad vdW isotermid ideaalgaasi isoterme, mis on kooskõlas sellega, et reaalgaasid käituvad ideaalsetena kõrgetel temperatuuridel ja madalatel rõhkudel.

TAHKISED

Sümmeetriateisendused ja sümmeetriaelemendid kristallograafias.

Sümmeetriateisendus on operatsioon, mille tulemusena kujundi võrdsed osad langevad kokku. Geomeetrilisi elemente, mille abil saab teostada sümmeetria​teisendusi, nimetatakse sümmeetriaelementideks (sm element- vähemalt 1 punkt jääb samasse kohta)

elemendid: sümmeetriatasand : jaotab kujundi kaheks võrdseks osaks, mis suhtuvad teineteisesse peegelpildid.

inversioonitsenter : punkt, millest läbi peegeldades kattub kujund iseendaga.

Sümmeetriatelg : sirge, mille ümber kujundi pööramisel elementaarnurga a võrra kujund kattub iseendaga.

Inversioonitelg :sirge, mille ümber kujundit teatud nurga võrra pöörates ja seejärel selle kujundi kõiki punkte läbi inversioonitsentri peegeldades kattub kujund iseendaga.

Süm teisendused: Translatsioon : süm teisendadus, mille käigus nihutatakse süsteemi paralleelselt teatud suuna ja kauguse võrra edasi nii, et sõlmed satuvad järgmiste sõlmede asemele.

Libiseva peegelduse tasand

Kruvitelg

Kristallvõret iseloomustavad suurused

2D struktuuri kirjeldamiseks on vaja 2 translatsioonivektorit a ja b, (mis määravad aatomitasandite vahelise kauguse) ning nendevahelist nurka, mida nim telgnurgaks

3D struktuuri kirjeldamiseks on vaja 3 translatsioonivektorit ning nendevahelisi võrenurki.

Võrebaas ja võre koordinatsiooniarv.

Lihtne, ruumtsentreeritud, tahktsentreeritud ja baastsentreeritud rakk.

Lihtne: aatomid asuvad võre sõlmpunktides

Ruumtsentreeritud: lihtne+ 1 aatom keskel

Tahktsentreeritud: lihtne+ 6 aatomit tahkudel

Baastsentreeritud: lihtne+ 2 aatomit vastastahkudel (Kas siis A, B või C-tahkudel)

Lihtrakkude (kuubiline, trigonaalne, tetragonaalne, heksagonaalne, ortorombiline, monoklinne, trikliinne) võrdlus nurkade erinevuse ja küljepikkuste erinevuse järgi ning nende eristamine eri liiki sümmeetriaelementide olemasolu alusel (Seda punkti võib seletada ka ilma nimesid kasutamata, aga on vaja ära tuua 7 Bravais’ võre põhimõte.

Kuubiline: a=b=c, nurgad 90

Trigonaalne: a=b?c, ?=?=90?, ?= mingi muu?

Tetragonaalne: a=b?c; ?=? =? =90?

Heksagonaalne: a=b?c, ?=?=90?, ?= 120?

Ortorombiline: a?b?c ?=?=?=90?

Monokliinne: a?b?c b=?=90???

trikliinne: a?b?c; ?????

Alumist tabelit pähe õppida siiski vaja pole; vaja teada, et Bravais võresid eristatakse süm elementide järgi.

Süsteem nõutavad sümmeetriaelemendid

Trikliinne puuduvad

Monokliinne 1 II järku (C ₂) telg

Rombiline 3 risti asetsevat II järku (C ₂) telge

Trigonaalne 1 III järku (C ₃) telg

Kuubiline 4 III järku (C ₃) telge

Tetragonaalne 1 IV järku (C ₄) telg

Heksagonaalne 1 VI järku (C ₆) telg

Aatomvõre, molekulvõre, ioonvõre ja metallilise võre iseloomustus ning võrdlus

Aatomvõrega kristallide sõlmpunktis paiknevad aatomid, mis on üksteisega seotud kovalentsete sidemetega. Tugev kovalentse sideme, seega väga tugevad ning üldiselt kõrge sulamistemperatuuriga ained. Juhivad halvasti elektrit

Molekulvõre moodustavad molekulid, mille vahel side nõrkade van der Waalsi jõududega. Tavaliselt tahkete orgaaniliste ühendite, CO2, tahkunud inertgaaside, väävli, fosfori jne puhul. Sublimeeruvad kergesti. Mehhaaniliselt- pehmed madala sul.temp-ga ained. Molekulvõred võivad olla väga keerulised. H-sidemed vm doonor-aktseptorsidemed mol vahel muudavad kristallvõre tugevamaks ja sul temp kõrgemaks.

Ioonkristallides elektrostaatilised jõud, mis toimivad kristallvõre sõlmpunktides vahelduvate positiivselt-negatiivselt laetud ioonide vahel. Ioonvõre enamasti soolade, oksiidide, hüdroksiidide korral. Ioonide ruumilise paigutuse määravad erinevate mõõtmetega kerade paigutusvõimalused võimalikult tihedalt, s.t et potentsiaalne energia oleks minimaalne. Kõrge sul temp

Metalliline võre ehitet katioonidest, mille vahel liiguvad elektronid (tekitavad keemilise sideme) Katioonid kristallvõre sõlmpunktides on paigutatud enamikel juhtudel tihedaima pakendi printsiibil, seega enamikul metallidest ongi kuubiline (ruumtsentreeritud/ tahktsentreeritud) või heksagonaalne võre. Juhivad elektrit, kõrge sul temp.

Aatomraadiuse ja võreparameetri suhe lihtsa, tahktsentreeritud ja ruumtsentreeritud kuubilise struktuuri korral

lihtne kuupvõre (K6) r = 0,5 a

ruumkesendatud kuupvõre (K8)

tahkkesendatud kuupvõre (K 12)

Selgita võre koordinatsiooniarvu määramist erinevate kuubiliste võrede, heksagonaalsete võrede korral.

Loe kokku lähimal võrdsel kaugusel asuvad aatomid kristallvõres.

Võreridade ja kristallograafiliste tasandite tähistamine kuubilises kristallivõres, Milleri indeksid.

Võresõlmede rea sümbol kirjutatakse nurksulgudesse nt [101]

Võretasandite kirjeldamiseks kasutatakse enamasti Milleri indekseid, mis on koordinaatide pöördväärtused transleeritud täisarvudeks. Indekseid tähistatakse (hkl), kirjelda ka, miks need head on (see lõpmatustega variant).

Määra joonisel toodud tasandi Milleri indeksid.

Määra joonisel toodud kristallstruktuui (hkl) indeksile vastav tasand.

Amorfsete ja kristalliliste tahkiste võrdlus. Ideaalsete monokristallide ja reaalsete kristallide võrdlus. Kristallvõredefektid.

Amorfseted ained on vedelikusarnased selles suhtes, et neil puudub kaugkorrapära, pole kristallvõre. Kristallides on see olemas. Amorfsetel ainetel pole kindlat sulamistemperatuuri, temperatuuri tõustes muutuvad nad aina rohkem vedelikusarnasteks. Kristallidel on kindel sul temp. Sarnaselt kristallidega amorfsed ained peaaegu ei voola.

Ideaalsetes monokristallides pole defekte; on tugevamad; entroopia on madal; ei sisalda sisestus ega asendusaatomeid,

DEFEKTID: punktdefektid : vakantsid: võivad tekitada võre deformatsiooni; migreeruda

võresõlmedevahelised aatomid : -//- saavad asuda oktaeedrilistes tühimikes

võõraatomid : asendus-, sisestusaatomid

lineaarsed defektid : paiknevad ühel joonel; nt vakantside/sõlmedevaheliste aatomite rida. Dislokatsioon: võredefetide kogum mingit joont pidi. Seda joont nim dislokatsioonijooneks. Nurkdislokarsioon: võretasandi katkemine kristalli sees.

Vintdislokatsioon: üks kristalli osa on nihkunud teise suhtes.

Pind-defektid : kristallvõredefektid, mis jooksevad võre 2 erineva orientatsiooniga piirkonna vahel.

Ruumilised defektid : tühikud suurema hulga võre sõlmpunktide asemel.

Kirjelda kuubilist tihepakendit ja heksagonaalset tihepakendit. Kirjelda aatomite vahele jäävate tühikute kuju. Selgita, miks nende tühikute suurus kristallograafias oluline on.

(Tahukeskne) kuubiline võre. I kiht: 1 aatomit ümbritseb 6;

II kiht: I kihi aatomite aukudes; (7 peale 3)

III kiht: II kihi aatomite tühimike peale (eelmise 3 peale jälle 3 nii, et kolmnurk vastupidine.

Heksagonaalne võre: III kiht: II kihi 3 aatomi keskele

Kuubilises tihepakendis tekivad oktaeedrilised ja heksagonaalses tetraeedrilised tühimikud. Tähtsad, sest sisestusaatomid mahuvad siis, kui tühimik piisavalt suur.

VEDELIKUD

Vedeliku ja reaalgaasi ja ideaalgaasi siserõhk. Siserõhu avaldise tuletamine, kasutades ühte Maxwelli seostest: (?T/?V)_S,n = -(?p/?S)_V,n; (?T/?p)_S,n = (?V/?S)_p,n; (?p/?T)_V,n = (?S/?V)_T,n ja (?V/?T)_p,n = -(?S/?p)_T,n.

Siserõhk näitab, kuidas muutub süsteemi siseenergia süsteemi paisumisel või kokkusurumisel konstantsel temperatuuril

Tuletuskäiku oskan.

Ideaalgaasi siserõhk = 0 ; reaalgaasi ja ka vedeliku (esimeses lähenduses) siserõhk on vdW võrrandi rõhu parandusliige (V_m kasutatakse; kuid seal vist pole vahet).

Vedelike võrdlus tahkiste ja gaasidega.

Tahkis ei võta anuma kuju ega täida seda. Gaas võtab anuma kuju ja täidab selle täielikult. Vedelik on tahkise ja gaasi vahepealne olek, mida iseloomustab kõrge viskoossus, sisehõõrdumine ja molekulidevaheline tugev toime. Kristalseid tahkiseid iseloomustab kaugkorrapära, vedelikes esineb osakeste paigutuses teatud ulatuses lähikorrapära, gaasidel korrapära puudub. Vedelikes on osakestel säilinud translatoorse liikumise vabadusastmed.

Gaasidega võrreldes on vedelikel tunduvalt suurem siserõhk, mistõttu on vedelikud raskesti kokkusurutavad.

Vedeliku, reaalgaasi ja ideaalgaasi siseenergia

Ideaalse gaasi siseenergia on kineetiline energia. See sõltub ainult temperatuurist, aga mitte ruumalast (1 mooli 1-aatomilise gaasi kineetiline energia Ekin = 3RT/2). Reaalsete gaaside ja vedelike korral lisandub sellele potentsiaalne energia, mis on tingitud molekulidevahelistest jõududest. Potentsiaalne energia sõltub nii temperatuurist kui ka molaarruumalast. Seega on reaalgaaside ja vedelike siseenergia sõltuv veel ka ruumalakoefitsendist e siserõhust. Siserõhk näitab, kuidas muutub süsteemi siseenergi selle kokkusurumisel/paisumisel konst temp juures.

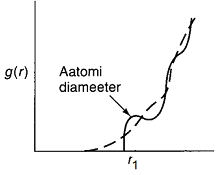
Lühi- ja kaugkorrapära kirjeldamine radiaalse jaotusfunktsiooni alusel. Erinevused tahkiste ja vedelike korral.

Lähikorrapära iseloomustatakse tavaliselt radiaalse jaotusfunktsiooni abil. Radiaalne jaotusfunktsioon näitab osakeste arvu mingil kindlal kaugusel r uuritavast punktist. (Kirjuta sellest, et tahkistel kaug ja vedelikes lähikorrapära. Radiaalse jaotusfun graafikud ja neid analüüsida ka. )

Osakeste keskmine arv ruumisosas dr tsentraalioonist kau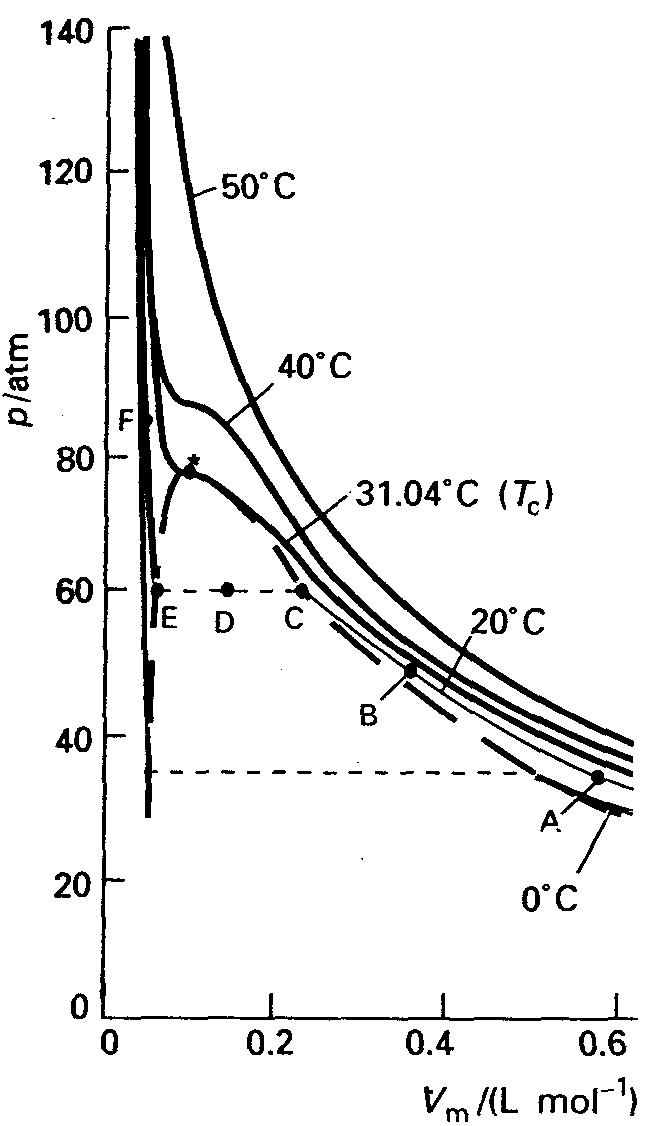gusel r on g(r)dr. Kui T  = 0, siis g(r)dr = N _r

Kui vedelikus valitseks täielik korrapäratus, siis oleks aatomite arv, mis jääb ruumiossa dr, võrdeline r ja

r + dr vahelise ruumiosa ruumalaga 4pii*r²dr, ehk seega võrdeline suurusega r². Sel juhul näeks radiaalse jaotuse diagramm kujutatav punktiiriga märgitud sõltuvusena. Pidev joon kujutab tegelikku sõltuvust. Nagu näha, langevad kõverad üsna hästi kokku suurematel kaugustel tsentraalioonist, ehk kaugemal korrapära puudub. Suur on reaalse sõltuvuse erinevus aga väikestel kaugustel, mis näitab lähikauguste struktuurset ülesehitust.

Van der Waalsi toimed.

Dip-dip; dip-induts dip; dispersioonijõud

Kaugtoimed ja lühitoimed, elektrostaatilised toimed ja molekulidevahelised (van der Waalsi) toimed ning nenede sõltuvus osakestevahelisest kaugusest.

Kaugtoimed:

ioon-ioon: sõltub pöördvõrdeliselt r-st

ioon-dipool: sõltub pöördvõrdeliselt raadiuse ruudust

ioon-induts dipool: sõltub pöördvõrdeliselt r astmel 4

dipool-dipool: sõltub pöördvõrdeliselt r astmel 6

dipool-indutseeritud

dipool toime: sõltub pöördvõrdeliselt r astmel 6

Dispersioonijõud: sõltub pöördvõrdeliselt r astmel 6

Lühitoimed:

tõukejõud: pöördvõrdeliselt r astmel “n”-st. Tavaliselt n=12

Vedelkristallid.

Vedelkristallid on ained, kus vähemalt ühes koordinaatsuunas on olemas ainult lähikorrapära elemendid ning vähemalt ühes või kahes ka kaugkorrastatud struktuur. Üks ots on polaarne; teine mittepolaarne Teatud tüüpi ühendid moodustavad nn smektilise faasi, millele on iseloomulik kihilise struktuuri olemasolu, st molekulid on orienteeritud ruumielemendis paralleelselt ja moodustavad kihte. Ained, mille molekulid on orienteeritud erinevate lineaarsete ahelatena ehk liinidena, moodustavad nemaatilise faasi. On olemas ka ühendid, mis moodustavad heeliksitaolisi struktuure (kolesteeriline faas), kus esinevad astmed ja augud ning sellistel vedelkristallidel esineb valguse difraktsiooninähtus.

nemaatiline smektiline kolesteeriline

Vedelkristalli ja selle konkreetsete struktuuride esinemine sõltub ka temperatuurist ning seetõttu on sageli tegemist erinevate vormide segudega.

TERMODÜNAAMIKA

Avatud, suletud ja isoleeritud süsteem. Adiabaatne ja diatermiline süsteem.

Avatud süsteem – toimub nii energia- kui ka ainevahetus ümbritseva keskkonnaga

Suletud süsteem – puudub ainevahetus ümbrusega, aga võib toimuda energiaülekanne kas töö (mehaaniline toime) või soojusena (termiline toime).

Isoleeritud süsteem – puudub nii energia- kui ka ainevahetus. Väliskeskkonnaga pole ei mehaanilist ega soojuslikku kontakti.

Diatermiline süsteem – soojusvahetus väliskeskkonnaga on võimalik

Adiabaatne süsteem – soojusvahetus väliskeskkonnaga puudub

Iseloomusta järgmisi protsesse/süsteeme: diatermiline, isotermiline, endotermiline, eksotermiline, adiabaatne. Selgita, kuidas muutub adiabaatses süsteemis eksotermilise protsessi korral temperatuur.

Diatermiline: soojusvahetus väliskeskkonnaga on olemas.

Isotermiline: temperatuur ei muutu protsessi käigus.

Endotermiline: soojust neelav protsess.

Eksotermiline: soojust eraldav protsess.

Adiabaatiline: süsteemil puudub soojusvahetus

Temp kasvab.

Selgita CaO ja CaCO₃ tasakaalu alusel, mis on komponentide arv, koostisosade arv ja seosevõrrand.

Koostisosad – süsteemis sisalduvad keemilised ühendid

Komponendid – üksteisest sõltumatud koostisosad, mille abil saab iseloomustada süsteemi kõiki faase ja ka süsteemi tervikuna. Komponentide arv = koostisosade arv – seosevõrrandite arv

Näiteks kui tasakaalus olev süsteem koosneb CaCO₃-st, CaO-st ja CO₂-st (koostisosast), siis komponentide arv on 2, sest neid aineid seob omavahel reaktsioonivõrrand

CaO + CO₂= CaCO₃

Mis on homogeenne ja heterogeenne süsteem ja mis on faas. Too näiteid.

Homogeenne süsteem – süsteem, mille omadused on tema kõigis osades ühesugused või muutuvad ühest kohast teise üleminekul pidevalt.

Heterogeenne süsteem – süsteem, mis koosneb mitmest erisuguste omadustega osast – faasist.

Faasid – süsteemis üksteistest ruumiliselt piirpindadega eraldatud ning omadustelt erinevad homogeensed osad. NB! Ühesuguste termodünaamiliste ja keemiliste omadustega süsteemiosad loetakse samaks faasiks ka siis, kui nad on üksteisest lahutatud eralduspindadega või asuvad osakestena teises faasis (näiteks jäätükid vees on üks tahke faas).

Olekuparameetrid, olekufunktsioonid, termodünaamilised funktsioonid, olekuvõrrandid.

Olekuparameetrid – suurused, millega saab termodünaamilise süsteemi olekut iseloomustada. Sõltumatuteks olekuparameetriteks võivad olla temperatuur T, rõhk p, mooliruumala Vm, kontsentratsioon c või moolide arv n, s.o füüsikaliselt mõõdetavad suurused.

Olekuvõrrand - Süsteemi olekut iseloomustavate parameetrite omavaheline sõltuvus (näiteks ideaalse gaasi olekuvõrrand, reaalse gaasi olekuvõrrand).

Olekufunktsioon – suurus, mis sõltub ainult süsteemi olekust, aga mitte selle oleku saavutamise viisist. Z = f(x, y) on olekufunktsioon, kui tema lõpmata väike muudatus dZ on täisdiferentsiaal:

Olekufunktsioone tähistatakse suurte tähtedega

Protsessifunktsioon – süsteemis toimuvat protsessi iseloomustav suurus, mis sõltub protsessi läbiviimise viisist (näiteks töö w, soojushulk q)

Termodünaamika I, II ja III seadus.

I: Energia ei teki ega kao vaid muundub ühest vormist teiseks

II: Isoleeritud süsteemi entroopia kasvab ajas.

III:Absoluutsel 0 temperatuuril on entroopiamuut 0 kui süsteemi on termodünaamilises tasakaalus

Paisumistöö, vaba paisumine, pöörduv ja mittepöörduv paisumine (selgita ka ideaalgaasi isotermi abil).

Paisumistöö üldvalem: dw=- pdV

Vaba paisumine, ehk paisumine vaakumisse. Kuna p _ex =0, siis ka w=0

Paisumine konstantse välisrõhu vastu: mittepöörduv paisumine, sest süsteem ei ole tasakaaluolekus.

Pöörduv paisumine: paisumise igal ajamomendil on süsteemi rõhk p võrdne välisrõhuga p_ex, st süsteem ei eemaldu tasakaaluolekust. +PV-GRAAFIK!!!

Soojusefektid konstantsel rõhul, ruumalal ja temperatuuril. Soojusefekti seosed siseenergia ja entalpiaga ideaalsete gaaside korral (tuletuskäigud, lähtudes termodünaamika I seadusest; mis on teisiti siis, kui tegemist ei ole ideaalse gaasiga?).

Lihtne.

Molekulide translatoorse, rotatoorse ja vibratsioonilise liikumise vabadusastmed.

Translatoorsed- 3

Rotatoorsed-

1-aatomiline gaas: r=0 (pole mingit vahet, millises suunas ta roteerub)

2-aatomiline gaas: r= 2 (dipooli teljega ristuva kahe koordinaattelje ümber)

3-aatomiline gaas: r= 3 (nii x, y kui ka z suunas roteerumine molekuli keskpunkti suhtes on erinev) VIBRATOORSE liikumise vabadusastmed tulevad mängu kõrgematel temp-l.

Ideaalgaasi siseenergia, entalpia ja soojusmahtuvuse molekulaarkineetiline tagapõhi

Lihtne.

Tuleta võrrand C_p = C_V + R. Milliste süsteemide korral see võrrand kehtib?

Lihtne.

Soojusmahtuvus, molaarne soojusmahtuvus ja erisoojusmahtuvus. Soojusmahtuvus konstantsel rõhul ja konstantsel ruumalal ning seosed olekufunktsioonidega. Ideaalsete ja reaalsete gaaside soojusmahtuvuse sõltuvus temperatuurist.

Lihtne, väikeses temp vahemikus võib lugeda soojusmahtuvuse konstantseks, erinevates piirkondades soojusmahtuvus erinev, ideaalgaasi soojusmahtuvus ei sõltu temp- liikumise vabadusastmetest sõltub.

Gaaside pöörduva isobaarilise paisumise töö, soojusefekt, entalpia ja siseenergia muut. Millised võrrandid kehtivad ideaalsete gaaside korral ja millised on universaalsed?

Lihtne.

Gaaside pöörduva isotermilise paisumise töö, soojusefekt, entalpia ja siseenergia muut. Millised võrrandid kehtivad ideaalsete gaaside korral ja millised on universaalsed?

Lihtne.

Pöörduva isokoorilise protsessi töö, soojusefekt, entalpia ja siseenergia muudud. Millised on erisused ideaalsete ja reaalsete gaaside korral?

Lihtne.

Gaaside pöörduva ja mittepöörduva isotermilise kokkusurumise töö, soojusefekt, entalpia ja siseenergia. Millised võrrandid kehtivad ideaalsete gaaside korral, millised on universaalsed?

Lihtne.

Pöörduva adiabaatse paisumise töö, soojusefekt, entalpia ja siseenergia muut. Temperatuuri ja ruumala seose (või T,p või V,p seose) tuletuskäik.

Temperatuuri ja ruumala seose tuletamine

Lähtume termodünaamika I seadusest ja deltaU avaldisest, arvestades, et q = 0. Saame

Eraldame muutujad:

Asendame R = C _p – C _v

jagame CV-ga (viime soojusmahtuvused ühte liikmesse):

Integreerides saame:

Hessi seadus ja selle rakendamine. Standardsed entalpiad.

Hessi seadus: Reaktsiooni soojusefekt sõltub süsteemi alg-ja lõppolekust, aga mitte protsessi läbiviimise viisist ega reaktsiooni vahestaadiumitest.

Reaktsiooni soojusefekti saame, kui produktide standardsete tekkeentalpiate summast lahutame lähteainete tekkeentalpiate summa, arvestades stöhhiomeetrilisi koefitsiente.

Standardne sidemeentalpia, põlemisentalpia, tekke-entalpia, sulamisentalpia, aurustumisentalpia....

Koosta võrrand Hessi seaduse alusel, et arvutada tundmatu reaktsiooni soojusefekti.

Koosta toodud protsesside entalpiate alusel Born-Haberi tsükkel, et arvutada tundmatu reaktsiooni soojusefekti.

Born-Haberi tsükkel koostatakse arvestusega, et ringprotsessi entalpiamuut on null, kuna alg- ja lõppolek on sama. Kui kogu tsükli ülejäänud etappide soojusefektid on teada, siis saab määrata selle etapi soojusefekti, mis pole veel teada.

Aine soojusmahtuvuse temperatuurisõltuvus.

Kui jätta välja väga madalad temperatuurid, siis on aine soojusmahtuvuse sõltuvus temperatuurist väljendatav ühega järgmistest võrranditest:

või

kus a, b, c ja c’ on ainele iseloomulikud suurused

On kindlaks tehtud, et madalatel temperatuuridel on soojusmahtuvuse temperatuurisõltuvus

C _p = const ? T ³ (Debye ekstrapolatsioon)

Mis on reaktsiooni soojusmahtuvus? Mis on reaktsiooni entalpia? Kuidas neid arvutada?

Keemilise reaktsiooni entalpia on soojusefekt, mis kaasneb keemilise reaktsiooniga (kui rõhk ja temperatuur ei muutu).

Keemiliste reaktsioonide soojusefekti arvutamine põhineb Hessi seadusel:

Reaktsiooni soojusefekt sõltub süsteemi alg- ja lõppolekust, aga mitte protsessi läbiviimise viisist ega reaktsiooni vahestaadiumidest.

Seega reaktsiooni soojusefekti saame, kui produktide standardsete tekkeentalpiate summast lahutame lähteainete tekkeentalpiate summa, arvestades stöhhiomeetrilisi koefitsiente.

Reaktsiooni soojusmahtuvus mingil temperatuuril on leitav analoogselt reaktsiooni entalpiamuuduga.

Integreerime võrrandit:

Saame võrrandi reaktsiooni soojusefekti arvutamiseks suvalisel temperatuuril, kui mingil temperatuuril on soojusefekt teada (Kirchoffi valem)

Üldjuhul sõltub reaktsiooni soojusmahtuvus temperatuurist ning selle sõltuvuse teadasaamiseks... loe konspekti :)

Reaktsiooni entalpia sõltuvus temperatuurist.

Kui temperatuur muutub, siis 1 mol aine entalpia muut dH=CpdT. See valem kehtib ka reaktsiooni entalpia ja soojusmahtuvustega Sealt saab avaldada reaktsiooni temperatuurikoefitsendi:

Kirchoffi seadus: Reaktsiooni soojusefekti temperatuurikoefitsent on võrdne reaktsioonist osavõtvate ainete C-de aritm summaga, arvestades stöhh koefitsente ning et lähteainete stöhh koefitsendid on neg. Integreerides saame:

Ainete soojusmahtuvused sõltuvad temp-st üldiselt kas

Koosta reaktsiooni entalpia avaldis, kui reaktsiooni soojusefekti temperatuurisõltuvus C _p = ?a + ?bT + ?cT ² (või C _p = ?a + ?bT + ?c’T^{- 2})

Reaktsiooni soojusefekt konstantsel rõhul ja konstantsel ruumalal, gaasireaktsioonide korral ning kondenseeritud süsteemides.

Kuna kondens süsteemides V ei muutu siis q võrdub nii U kui ka H ga; gaasides on soojusefekt konst ruumalal deltaU ja konst rõhul deltaH

Carnot´ ringprotsess, erinevate etappide töö, soojusefekt, siseenergia ja entalpia muudud.

Tõesta, et Carnot’ ringprotsessi ruumalade jagatised on võrdsed (V_B/V_A=V_C/V_d).

Pöörduva adiabaatilise protsessi korral

Kui vabastame ruumalad astendajatest, siis:

Kirjutame analoogsed võrrandid ringprotsessi kahe adiabaatilise osa kohta:

Korrutame kaks võrrandit omavahel ja saame

Kuna temperatuuriliikmed saame taandada, siis

Carnot’ ringprotsessi üldiseloomustus ja olulisus. Tõesta, et Carnot ringprotsess teeb tööd.

Summaarne töö:

w _ring= -RT _soeln

-RT _külm

Kuna

siis

ln

järelikult

w _ring = -RT _soeln +RT _külmln

w _ring = (T _külm-T _soe)R ln

Kuna V _B > V _A, siis logaritmiliige positiivne. Kuna T _soe > T _külm, siis on temperatuuride vahe võrrandis negatiivne, seega

w _ring < 0 Järelikult teeb Carnot’ ringprotsess tööd.

Carnot’ ringprotsess teeb tööd (w < 0), kuid see töö on palju väiksem soojushulgast qsoe, mille arvelt see töö tehakse. Carnot’ ringprotsess näitab, et põhimõtteliselt ei saa kogu soojust muundada tööks.

Carnot’ ringprotsessi kasutegur on alati väiksem 1-st.

Pöörduva protsessi kasutegur on maksimaalseim võimalikest ja sõltub ainult temperatuuride erinevusest.

Mittepöörduva protsessi kasutegur on väiksem pöörduva protsessi kasutegurist.

Tõesta, et Carnot’ ringprotsessi kasutegur on väiksem ühest.

Kuna w = –(q _soe + q _külm), siis

(Absoluutväärtuse märgid on selleks, et w < 0, aga negatiivsest kasutegurist me ei räägi.) Asendame soojushulgad nende avaldistega:

Kuna T _soe – T _külm < T _soe,

siis ? < 1

Kirjelda energia hajumist, selle termodünaamilist tagapõhja ning seda, kuidas on energia hajumine kooskõlas td. I seadusega.

Oletame, et keha energiatihedus on keskkonna omast kõrgem. Keha annab osa energiast ümbritsevale keskkonnale (energia hajub). See ei ole vastuolus termodünaamika I seadusega, mis kehtib isoleeritud süsteemi kohta. Kui vaatleme keha ja keskkonda tervikuna isoleeritud süsteemina, siis jääb kogu süsteemi energiahulk samaks, kuid ei ole võimalik spontaanse protsessi abil energiat uuesti keskkonnast kehasse kontsentreerida.

Pöörduva ja mittepöörduva ringprotsessi entroopia (võrdlus!) ning selle seos soojusefektiga.

Kuna mittepöörduva isotermilise protsessi töö on alati väiksem kui pöörduva protsessi töö, siis

kus vasakpoolne mittepöörduva ning parempoolne osa samas temperatuurivahemikus töötava pöörduva protsessi kasutegurit. Pöörduvalt töötava ringprotsessi korral

siis järelikult mittepöörduva ringprotsessi

Siin ei ole tegemist isoleeritud süsteemiga, sest toimub väliskeskkonnaga soojusvahetus. Kuna entroopia on olekufunktsioon, siis entroopiamuutus tsüklis peab igal juhul olema 0, olenemata sellest, kas jõuame punktist A punkti A pöörduva või mittepöörduva protsessi abil.

? ?S _{rev ringprotsess} = ?S _{irr ringprosess} =

?

Entroopia muutus pöörduvates ja mittepöörduvates protsessides.

Pöörduva protsessi summaarne entroopiamuut isoleeritud süsteemis on null .

Kui paisumine toimub vabalt ja mittepöörduvalt (kui temperatuur ei muutu ja tööd ei tehta), siis ümbritsev keskkond soojust ei saa ja ja tema entroopiamuut on null:

?S _keskkond= 0

ning summaarne entroopiamuut:

Mittepöörduva protsessi summaarne entroopia muut isoleeritud süsteemis on positiivne

Entroopia muutus iseeneslikes (mittepöörduvates) protsessides. Entroopia kasvu seadus.

Mittepöörduva protsessi summaarne entroopia muut isoleeritud süsteemis on positiivne

Tuleta entroopia avaldis ideaalgaasi jaoks td. I seadusest ning sellest edasiarendus kas p ja T või p ja V kaudu avaldiseks. Analüüsi võrrandeid, kui üks kolmest parameetrist (p, V või T) on konstantne.

S avaldisest saab tuletada valemeid erinevates tingimustes kasutamiseks:

?Kui on isotermiline protsess, siis

?Kui on isokooriline protsess, siis

Kui on isobaariline protsess, siis

Segunemisprotsess: Tuleta segunemisentroopia avaldis, analüüsi valemi põhjal segunemise isevoolulisust ning entroopia muutust (analüüsida peab oskama ka ilma tuletuskäiguta).

Olgu meil kahe erineva gaasiga täidetud reservuaari, kus ruumalad ja ainehulgad on erinevad, temperatuur ja rõhk aga samad:

p ₁ = p ₂

T ₁ = T ₂

Kui need reservuaarid ühendada, siis gaasid segunevad. Arvestades, et gaasid on ideaalsed ning et kehtib Daltoni seadus, saame kirjutada entroopiamuudud kummagi gaasi kohta:

Kuna p ja T ei muutu, siis saame ideaalse gaasi olekuvõrrandi põhjal ruumalade liikmed asendada moolmurdudega:

Kogu segunemise entroopia on:

Kuna

X ₁

Entroopia arvutamine laias potentsiaalide vahemikus, kui vahepeal toimuvad ka faasilised muundused.

Entroopia temperatuurisõltuvuse avaldise saame järgmiselt:

kus C on kas Cp isobaarilise protsessi või CV isokoorilise protsessi korral.

Integreerides saame

Võrrandi lahendamiseks laias temperatuurivahemikus peame teadma, milline on soojusmahtuvuse temperatuurist sõltuvus.

Faasilise üleminekute korral : kui rõhk protsessi käigus ei muutu, siis on soojushulk võrdne faasilise ülemineku entalpiamuuduga, seega saame kirjutada näiteks sulamisentroopia avaldise:

Konstantsel rõhul toimuva reaktsiooni soojusefekt kitsas ja laias temperatuurivahemikus. Faasilise ülemineku soojusefekt.

Kitsas temp vahemikus võib reaktsiooni soojusefekti lugeda konstantseks.

Laias tempetatuurivahemikus on reaktsiooni soojusefekt konstantsel rõhul ehk teisisõnu ENTALPIA, arvutatav Kirchoffi valemi järgi.

Faasilise ülemineku soojusefektid on konkreetse aine ühikulise koguse ja kindla faasilise ülemineku jaoks fikseeritud suurused : sulamissoojus, aurustumissoojus...

Termodünaamiliste potentsiaalide avaldised, kui süsteem ei tee kasulikku tööd (tuletuskäikudega).

Võtame aluseks entalpia definitsioonfunktsiooni

Selle põhjal on entalpia muutus avaldatav kujul

Asendame dU tema avaldisest

ning koondame sarnased liikmed.

Süsteemi vaba ja seotud energia ning nende seos süsteemi siseenergia ja entalpiaga.

dU = dF + TdS Seega koosneb süsteemi siseenergia kahest osast: nn vabast energiast F ja seotud energiast TS. Vabaenergia väljendab süsteemi töövõimet, sest seda võib muuta pöörduva protsessi korral täielikult tööks. Seotud energiat ei saa muuta tööks:TdS on entroopia definitsioonvalemi järgi protsessi käigus eraldunud soojushulk. Seda osa siseenergiast ei ole võimalik muuta tööks.

dH = dG + TdS

Gibbsi energia sõltuvus rõhust (tuletuskäiguga).

Kui võtta temperatuur konstantseks, siis saame:

Kondenseeritud süsteemide (vedelikud ja tahkised) korral on mooliruumalad väikesed ning ei sõltu praktiliselt rõhust ning seetõttu pole neis süsteemides vaja Gibbsi energia rõhust sõltuvust arvestada.

Oluliselt sõltub Gibbsi energia rõhust aga gaaside korral. Kui tegemist on ideaalgaasiga, siis saame ruumala (mis sõltub rõhust) avaldada ideaalgaasi olekuvõrrandist:

Integreerimisel saame leida Gibbsi energia muudu üleminekul olekust 1 (p1) olekusse 2 (p2).

Kui võtta algolekuks standardolek, siis saame

Gibbsi energia rõhust sõltuvuse avaldise saab kirjutada ka reaalgaaside korral, kui kasutada fugitiivsusi (f), st viia võrrandisse aktiivsuskoefitsient gamma, mis arvestab gaasi omaduste erinevust ideaalgaasist:

f= ?p

Gibbsi energia sõltuvus temperatuurist (tuletuskäiguga).

Kui süsteem läheb ühest olekust teise, siis saab kirjutada vastava seose Gibbsi energia ja entroopia muutuste vahel:

ning Gibbsi energia definitsioonvõrrandist

saame avaldada deltaS:

Asendame ?S ja korraldame võrrandi ümber:

Võrrandi vasaku poole asendamiseks leiame liikmest ?G/T tuletise T järgi vastavalt mitme muutuja reeglile:

millest pärast temperatuuriga korrutamist ja ümberkorraldusi saame:

Asendame valemis (1) vasaku poole saadud avaldisega:

Viime temperatuuri vasakult paremale ja saame Gibbs-Helmholtzi võrrandi:

Arvutustes kasutamiseks on seda võrrandit vaja integreerida:

Gaasi keemiline potentsiaal standardne keemiline potentsiaal. Keemilise potentsiaali seos gaasi rõhu, aktiivsuse, fugitiivsuse ja aktiivsuskoefitsiendiga.

Aine keemiline potentsiaal näitab, kuidas muutub süsteemi Gibbsi energia, kui ainehulk muutub 1 mooli võrra

Oletame, et meil on tegemist gaasireaktsiooniga ja gaasid käituvad ideaalgaasidena. Sel juhul saab iga konkreetse aine kohta kasutada järgmist G rõhust sõltuvuse avaldist:

kus p ^? on standardrõhk (1 bar)

Asendame Gibbsi energiad vastavate keemiliste potentsiaalidega, siis saame aine i keemilise potentsiaali muutuse üleminekul standardolekust mingisse teise olekusse:

Kui võtame gaaside segu üldrõhu p võrdseks 1 baariga ehk oletame, et süsteem on standardrõhul, sel juhul saame rõhkude suhte asendada gaasi aktiivsustega süsteemis:

järelikult:

Keemilise reaktsiooni tasakaalu ja suuna kriteeriumid.

(1) dH<0, dS>0, suvaline T

(2) dH<0, dS<0, madal T

(3) dH>0, dS>0, kõrge T

n1

V1

n2

V2